三门峡网站设计_公司网站建设申请报告_qq营销软件_互联网营销方式

引入GRU和LSTM的原因是：RNN在实践中常见的问题是：数值不稳定性；虽然在前面已经应用了梯度裁剪等技术缓解这个问题，但是我们还是需要通过设计更复杂的序列模型处理这个问题。
出现GRU和LSTM的原因：应对以下问题：

早期观测值对预测所有的未来观测值有很重要的意义
一些词元没有相关的观测值；eg:在对网页内容进行情感分析时，可能有一些辅助HTML代码与网页传达的情绪无关。在这种情况下，我们希望有一些机制来跳过隐状态表示中的此类词元。
序列的各个部分之间存在逻辑中断；eg:书的章节之间可能会有过渡存在，或者证券的熊市和牛市之间可能会有过渡存在。在这种情况下,最好有一种方法来重置我们的内部状态表示。

GRU和LSTM的关系：GPU是LSTM的稍微简化的变体；通常提供同等的效果；计算速度明显更快；更简单。

门控循环单元（GRU）

门控隐状态

引入

门控循环单元和普通的循环神经网络之间的关键区别是：门控循环单元支持隐状态的门控,具体指：模型有专门的机制确定何时更新隐状态；何时重置隐状态（这个机制是可学习的）；eg:如果第一个词元非常重要，模型将学会在第一次观测之后不更新隐状态。同样，模型也可以学会跳过不相关的临时观测。最后，模型还将学会在需要的时候重置隐状态。

重置门和更新门

重置门和更新门的功能：

重置门（ reset gate）：控制“可能还想记住”的过去状态的数量
更新门（update gate）：控制新状态中有多少个是旧状态副本

重置门和更新门构造

输入：当前时间步的输入和前一时间步的隐状态给出。
输出：使用sigmoid激活函数的2个全连接层给出。
图像化：
重置门和更新门数学表示：

都是（0，1）区间中的向量；
变量含义：
$X_{t}$ $\epsilon$ $\mathbb{R}^{n\cdot d}$ (样本个数n，输入个数d)：输入；
$H_{t-1}$ $\epsilon$ $\mathbb{R}^{n\cdot h}$ (隐藏单元个数h）：上个时间步的隐状态；
$R_{t}$ $\epsilon$ $\mathbb{R}^{n\cdot h}$ :重置门；
$Z_{t}$ $\epsilon$ $\mathbb{R}^{n\cdot h}$ :更新门；
$W_{x r}$ , $W_{x z}$ $\epsilon$ $\mathbb{R}^{d\cdot h}$ ,, $W_{h r}$ , $W_{h z}$ $\epsilon$ $\mathbb{R}^{h\cdot h}$ :权重参数；
$b_{r}$ , $b_{z}$ $\epsilon$ $\mathbb{R}^{1\cdot h}$ :偏置参数
具体公式如下：

候选隐状态（candidate hidden state）

变量含义：
$\tilde{H}_{t}$ $\epsilon$ $\mathbb{R}^{n\cdot h}$ ：候选隐状态；
$W_{x h}$ $\epsilon$ $\mathbb{R}^{d\cdot h}$ , $W_{h h}$ $\epsilon$ $\mathbb{R}^{h\cdot h}$ :权重参数；
$b_{h}$ $\epsilon$ $\mathbb{R}^{1\cdot h}$ :偏置项；
$\odot$ ：Hadamard积（按元素乘积）运算符
tanh:tanh非线性激活函数，作用：确保隐状态中的值保持在区间（-1，1）中

下图是常规隐状态的公式：

$\tilde{H}_{t}$ $\epsilon$ $\mathbb{R}^{n\cdot h}$ = $R_{t}$ 和常规隐状态的集成；具体公式如下：

对候选隐状态具体公式的解析：

$R_{t}$ , $H_{t-1}$ 的元素相乘可以减少以往状态的影响
当 $R_{t}$ 接近1，候选隐状态 = 常规隐状态；当 $R_{t}$ 接近0，候选隐状态则是输入为 $X_{t}$ 的多层感知机的结果

下图为应用reset gate之后的计算流程：

更新门 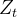$Z_{t}$

更新门 $Z_{t}$ 功能：确定新的隐状态 $H_{t}$ $\epsilon$ $\mathbb{R}^{n\cdot h}$ 多大程度来自旧的状态 $H_{t-1}$ 和新的候选状态 $\tilde{H}_{t}$ ,
更新门 $Z_{t}$ 具体做法：在 $H_{t-1}$ 和 $\tilde{H}_{t}$ 之间按元素的凸组合；当 $Z_{t}$ 接近1，模型倾向只保留旧状态，基本忽略来自 $X_{t}$ ，有效跳过依赖链条中的时间步t,当 $Z_{t}$ 接近0，新的隐状态 $H_{t}$ 就会接近候选隐状态 $\tilde{H}_{t}$
更新门 $Z_{t}$ 功能的优势：

有助于处理RNN中的梯度消失问题；
捕获时间步距离很长的序列的依赖关系。

隐状态

隐状态=候选隐状态结合更新门 $Z_{t}$ ，具体公式（门控循环单元的最终更新公式）如下：

综上所述可知：

reset gate：有助于捕获序列中的短期依赖关系；
update gate：有助于捕获序列中的长期依赖关系

GRU具体代码如下：

长短期记忆网络（LSTM)

LSTM适用于解决隐变量模型中的问题：长期信息保存，短期输入缺失
LSTM和GRU之间的关系：

与GRU有许多相同的属性；
比GRU稍微复杂一些
比GRU早诞生近20年

LSTM设计灵感：计算机的逻辑门

门控记忆元

基本概念：

记忆元（memory cell）（单元（cell））：是隐状态的一种特殊类型；与隐状态具有相同的形状；目的：记录附加的信息。
控制记忆元的门：

输入门（input gate）：决定何时将数据读入单元
输出门（output gate）：用来从单元中输出条目
遗忘门（forget gate）：重置单元的内容，控制保留多少过去的记忆元的内容（和GRU的重制门功能一样）

输入门、忘记门、输出门构造

输入：当前时间步的输入和前一个时间步的隐状态
门计算主体：具有sigmoid激活函数的全连接层
三个门的值的范围：（0，1）
三个门的实际计算流程图如下：

LSTM数学表达

变量含义：

h:隐藏单元
n: 批量大小
d:输入数
$X_{t}$ $\epsilon$ $\mathbb{R}^{n\cdot d}$ :输入
$H_{t-1}$ $\epsilon$ $\mathbb{R}^{n\cdot h}$ :前一时间步的隐状态
$I_{t}$ $\epsilon$ $\mathbb{R}^{n\cdot h}$ :输入门：控制采用多少来自 $\tilde{C_{t}}$ 的新数据
$F_{t}$ $\epsilon$ $\mathbb{R}^{n\cdot h}$ :遗忘门：控制保留多少过去的记忆元 $C_{t-1}$ $\epsilon$ $\mathbb{R}^{n\cdot h}$ 的内容
$O_{t}$ $\epsilon$ $\mathbb{R}^{n\cdot h}$ :输出门
$W_{x i}$ , $W_{x f}$ , $W_{x o}$ $\epsilon$ $\mathbb{R}^{d\cdot h}$ 和 $W_{h i}$ , $W_{h f}$ , $W_{h o}$ $\epsilon$ $\mathbb{R}^{h\cdot h}$ :权重参数
$b_{i}$ , $b_{f}$ , $b_{o}$ :偏置参数

门控的计算表达式：

候选记忆元（candidate memory cell）

candidate memory cell数学表达

变量含义：

$\tilde{C_{t}}$ $\epsilon$ $\mathbb{R}^{n\cdot h}$ :candidate memory cell
$W_{x c}$ $\epsilon$ $\mathbb{R}^{d\cdot h}$ , $W_{h c}$ $\epsilon$ $\mathbb{R}^{h\cdot h}$ :权重参数
$b_{c}$ $\epsilon$ $\mathbb{R}^{1\cdot h}$ :偏置参数

candidate memory cell在时间步t处的方程：

候选记忆元在长短期记忆模型的运作图如下：

记忆元 $C_{t}$

$C_{t}$ 的表达式：

如上式可知， $F_{t}$ （遗忘门）始终等于1， $I_{t}$ （输入门）始终等于0，则记忆元 $C_{t-1}$ 随着时间被保存并传递到当前时间步（这样，可以缓解梯度消失，并更好地捕获序列中的长距离依赖关系）

计算记忆元的流程图如下:

隐状态 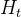$H_{t}$ $\epsilon$ $\mathbb{R}^{n\cdot h}$

在长期记忆网络中，隐状态是记忆元的tanh的门控版本，隐状态的值始终在区间（-1，1）内，具体表达式如下：

根据上述公式，我们可知：输出门（ $O_{t}$ ）接近1，能有效地将所有记忆信息传递给预测部分； $O_{t}$ 接近0，只保留记忆元的所有信息，不需要更新隐状态。

数据流的图形化演示如下：

LSTM具体代码如下：

深度递归神经网络

深度循环神经网络具有多个隐藏层，每个隐状态都连续传递到当前层的下一个时间步和下一层的当前时间步

下图为深度循环神经网络结构：

基于上图深度循环神经网络结构的函数依赖关系如下：

变量含义：

$X_{t}$ $\epsilon$ $\mathbb{R}^{n\cdot d}$ (样本数：n, 每个样本中的输入数：d):（一个小批量）输入数据
$l^{t h}$ (l=1, ..., L):隐藏层
$H^{ (l) }_{t}$ $\epsilon$ $\mathbb{R}^{n\cdot h}$ (隐藏单元数：h): $l^{t h}$ 隐藏层的隐状态
$O_{t}$ $\epsilon$ $\mathbb{R}^{n\cdot q}$ (输出数：q):输出层变量
假设： $H^{ (0)}_{t}$ = $X_{t}$ ;第l个隐藏层的隐状态使用激活函数 $\phi _{l}$
$W^{(l)}_{x h}$ $\epsilon$ $\mathbb{R}^{h\cdot h}$ , $W^{(l)}_{h h}$ $\epsilon$ $\mathbb{R}^{h\cdot h}$ :第l个隐藏层的模型权重
$b_{h}^{(l)}$ $\epsilon$ $\mathbb{R}^{1\cdot h}$ :第l个隐藏层的模型偏置

隐状态表达式：

输出层表达式（基于第l个隐藏层最终的隐状态）：

其中，隐藏层数目L，隐藏单元数目h都是超参数
将上面深度循环神经网络的隐状态换成GRU,LSTM的隐状态就能得到深度门控循环神经网络或深度长短期记忆神经网络

深度递归神经网络具体实现代码如下：

双向循环神经网络

隐变量更新的数学知识--隐马尔可夫模型中的动态规划

以下的概率图模型是--隐马尔可夫模型（hidden Markov model， HMM）（隐变量模型），

具体变量含义如下：

t:任意时间步
$h_{t}$ :某个隐变量
P（ $h_{t}$ | $h_{t-1}$ ）：从时刻t-1的隐状态 $h_{t-1}$ 转移到时刻t的隐状态 $h_{t}$ 的转移概率；描述了隐状态之间的动态变化规律
P（ $x_{t}$ | $h_{t}$ ）：给定时刻t的隐状态 $h_{t}$ 的条件下，观测到 $x_{t}$ 的概率（发射概率）；建立了隐状态和观测值之间的联系

HMM具体模型图如下：

根据上述HMM模型图，我们可以得出：对于T个观测值的序列，在观测状态和隐状态上具有以下联合概率分布：

对上述的联合概率分布，我们有以下2种计算方式：前向递归；后向递归

前向递归：

通常，前向递归（forward recursion）写为

前向递归初始化为 $\pi _{1}$ （ $h_{1}$ ）=P( $h_{1}$ );前向递归符号简化为 $\pi _{t+1}$ =f( $\pi _{t}$ , $x_{t}$ )，这个前向递归符号简化式像我们在循环神经网络中讨论的隐变量模型中的更新方程；f：一些可学习的函数；

后向递归：

通常，后向递归（backward recursion）写为

后向递归初始化为 $\rho _{T}$ （ $h_{T}$ ）=1；后向递归符号简化为 $\rho _{t-1}$ =g( $\rho _{t}$ , $x_{t}$ );这个前向递归符号简化式像我们在循环神经网络中讨论的隐变量模型中的更新方程；g：一些可学习的函数；

对forward recursion和backward recursion的总结如下：

都允许对T个隐变量在 $\bigcirc$ （kT）（线性，不是指数）时间内对（ $h_{1}$ ,..., $h_{T}$ ）的所有值求和
结合forward recursion和 backward recursion，计算下式：

由上，我们可知HMM有前瞻能力

双向循环神经网络（bidrectional RNNs)

bidrectional RNNs具有HMM的类似前瞻能力：添加了反向传递信息的隐藏层
下面是具有单个隐藏层的双向循环神经网络的架构：

这个构架的思想和HMM的forward recursion和backward recursion没有大区别，主要的区别是：HMM的方程具有特定的统计意义； bidrectional RNNs没有这样容易理解的解释，我们只能把它们当作通用、可学习的函数。 bidrectional RNNs的这种转换集中体现现代深度网络的设计原则：1.使用经典统计模型的函数依赖类型；2.将其参数化为通用形式。

bidrectional RNNs数学表达：

变量含义：

n:样本数；
d:(每个示例中的）输出数;
$X_{t}$ $\epsilon$ $\mathbb{R}^{n\cdot d}$ :给定一个小批量的输入数据
$\phi$ ：隐藏层激活函数
h:隐藏单元的数目
q:输出单元的数目
$\vec{H}_{t}$ $\epsilon$ $\mathbb{R}^{n\cdot h}$ :该时间步的前向隐状态
$H ^{\leftarrow }_{t}$ $\epsilon$ $\mathbb{R}^{n\cdot h}$ ：该时间步的反向隐状态
$W^{(f)}_{x h}$ $\epsilon$ $\mathbb{R}^{d\cdot h}$ , $W^{(f)}_{h h}$ $\epsilon$ $\mathbb{R}^{h\cdot h}$ , $W_{x h}^{(b)}$ $\epsilon$ $\mathbb{R}^{d\cdot h}$ , $W_{h h}^{(b)}$ $\epsilon$ $\mathbb{R}^{h\cdot h}$ , $W_{h q}$ $\epsilon$ $\mathbb{R}^{2h\cdot q}$ :模型权重
$b_{h}^{(f)}$ $\epsilon$ $\mathbb{R}^{1\cdot h}$ , $b_{h}^{(b)}$ $\epsilon$ $\mathbb{R}^{1\cdot h}$ , $b_{q}$ $\epsilon$ $\mathbb{R}^{1\cdot q}$ :模型偏置
$H_{t}$ $\epsilon$ $\mathbb{R}^{n\cdot 2h}$ :是 $\vec{H}_{t}$ 和 $H ^{\leftarrow }_{t}$ 连接产物；是送入输出层的隐状态
$O_{t}$ $\epsilon$ $\mathbb{R}^{n\cdot q}$ :输出层的输出

forward 和backward隐状态更新公式如下：

forward recursion和backward recursion可以拥有不同数量的隐藏单元。

输出层的输出公式如下：

bidrectional RNNs的一个关键特性：用序列两端的信息估计输出；用过去和未来的观测信息来预测当前的观测。这个关键特性使得bidrectional RNNs在预测下一个词元的场景中，效果不好（因为不知道下一个词元的下文是什么，所以精度很差）
bidrectional RNNs还一个严重问题：计算速度非常慢（因为网络的forward需要在双向层中进行forward recursion和backward recursion，网络的反向传播还依赖于forward的结果，这样就会导致梯度求解有一个非常长的链）
bidrectional RNNs在一些场景的应用：填充缺失的单词；词元注释（用于命名实体识别）；作为序列处理流水线的一个步骤对序列进行编码（eg:用于机器翻译）

bidrectional RNNs的具体代码如下：

机器翻译与数据集

机器翻译（machine translation）

machine translation的重要性：machine translation是语言模型最成功的基准测试，语言模型是NLP的关键；也是将输入序列转换成输出序列的序列转换模型（sequence transduction）的核心问题。
machine translation概念：将序列从一种语言自动翻译成另外一种语言
machine translation分类：statistical machine translation（统计机器翻译）；neural machine translation（神经机器翻译）（强调端到端的学习）
machine translation的数据集：由源语言和目标语言文本序列对组成的
machine translation预处理machine translation dataset方法（这个方法不是复用语言模型的预处理程序）：

下载数据集
进行具体预处理：用空格代替不间断空格；用小写字母替换大写字母；在单词和标点符号之间插入空格

machine translation预处理数据集的代码如下：

词元化

在机器翻译中，我们喜欢单元级词元化，一个词元是一个词或者是一个标点符号；具体代码如下：

使用一些规则缩小字符级词元表，规则为：将出现次数少于2次的低频率词元视为相同的未知(“<unk>”)词元；指定额外的特定词元，eg:在小批量时用于将序列填充到相同长度的填充词元(“<pad>”)，以及序列的开始词元(“<bos>”)和结束词元“<eos>”)。(这些特殊词元在自然语言处理任务中比较常用。);具体代码如下：

读取数据集

读取数据集具体代码如下：

编码器-解码器架构

编码器-解码器架构构成的目的：为了处理机器翻译产生的长度都是可变的输入和输出
编码器，解码器分别的功能：

编码器：接受一个长度可变的序列作为输入，将其转换成固定形状的编码状态
解码器：将固定形状的编码状态映射到长度可变的序列

编码器-解码器架构图：

以英语到法语的机器翻译为例，解释上述架构图：给定一个英文的输入序列:“They”“are”“watching”“.”。编码器-解码器架构过程：

首先，“编码器一解码器”架构将长度可变的输入序列编码成一个“状态”，
然后对该状态进行解码，一个词元接着一个词元地生成翻译后的序列作为输出:“Ils”“regordent”“.”。

编码器-解码器架构具体代码如下：

机器翻译的序列到序列学习

使用2个循环神经网络的编码器和解码器的核心思路：循环神经网络的编码器使用长度可变的序列作为输入，将其转换为固定形状的隐状态；循环神经网络的解码器基于输入序列的编码信息和输出序列已经看到的或者生成的词元来生成输出序列的词元
使用循环神经网络的编码器-解码器架构图：

对使用循环神经网络的编码器-解码器架构图解析：

序列结束词元：<eos>，作用：模型预测的停止标志
循环网络解码器的初始化时间步：

解码器的输入序列的第一个词元：<bos> , 作用：序列开始的标志词元
使用循环网络编码器的隐状态初始化解码器的隐状态

编码器

变量含义：

c:形状固定的上下文变量
$x_{1}$ ,..., $x_{T}$ :输入序列
$x_{T}$ :输入文本序列中的第t个词元
$x_{t}$ ：时间步t处的词元 $x_{t}$ 的输入特征向量
$h_{t-1}$ :上一时间步的隐状态
$h_{t}$ ：当前时间步的隐状态

核心思路：

将长度可变的输入序列转换成形状固定的上下文变量c,并将输入序列的信息在该上下文变量中进行编码。

函数f:描述循环神经网络的循环层所做的变换

函数q:将所有时间步的隐状态转换为上下文变量

核心公式：

$h_{t}$ =f( $x_{t}$ , $h_{t-1}$ )

c=q( $h_{1}$ ,..., $h_{T}$ )

具体代码如下：

解码器

变量含义：

c:形状固定的上下文变量
$y_{1}$ , $y_{2}$ ,... $y_{{T}'}$ :训练数据集的输出序列
${t}'$ :时间步（与编码器的输入序列不同）
$y_{1}$ ，..., $y_{{t}'-1}$ :先前的输出子序列
P（ $y_{{t}'}$ | $y_{1}$ ,..., $y_{{t}'-1}$ ,c）:解码器输出概率 $y_{{t}'}$

核心思路：

使用另一个循环神经网络作为解码器。在输出序列上的任意时间步 ${t}'$ ，上一时间步的输出 $y_{{t}'-1}$ 和上下文变量c作为解码器的输入，在当前时间步将输入和上一隐状态 $s_{{t}'-1}$ 转换为隐状态 $s_{{t}'}$ 。然后使用输出层和softmax操作计算在时间步 ${t}'$ 时输出 $y_{{t}'}$ 的条件概率分布P（ $y_{{t}'}$ | $y_{1}$ ,..., $y_{{t}'-1}$ ,c）

函数g:(解码器的隐藏层变换） $s_{{t}'}$ =g( $y_{{t}'-1}$ ，c， $s_{{t}'-1}$ )

具体代码如下：

将编码器和解码器放在一起

束搜索

定义搜索问题：在任意时间步 ${t}'$ ,解码器输出 $y_{{t}'}$ 的概率取决于时间步 ${t}'$ 之前的输出子序列 $y_{1}$ ，..., $y_{{t}'-1}$ 和对输入序列的信息进行编码得到的上下文变量c。
变量含义：
y(是个阿拉伯数字形式，笔者文字编辑能力有限，编辑不出来😭，不过不影响阅读哈，就是不够准确😭）：输出词表，（输出词表包含“<eos>”) |y|:词汇集合的基数，表示：词表的大小
${T}'$ ：输出序列的最大词元数
束搜索目标：从所有O( $|y|^{{T}'}$ )个可能的输出序列中寻找理想的输出。 ps:对于所有输出序列，在“<eos>”之后的部分（非本句）将在实际输出中丢弃。

贪心搜索

基本思想：对于输出序列的每一时间 ${t}'$ ，我们都将基于贪心搜索从y中找到具有最高条件概率的词元。该词元数学表达式如下：
贪心搜索输出完成标志：1.输出序列包含“<eos>”; 2.达到输出序列最大长度 ${T}'$
贪心搜索弊端：无法保证得到最优序列
举例说明贪心搜索弊端：

最优序列（optimal sequence）：最大化 $\prod _{{t}'=1}^{{T}'}$ P( $y_{{t}'}$ | $y_{1}$ ,..., $y_{{t}'-1}$ ,c)值的输出序列（是基于输入序列生成输出序列的条件概率）

例1：在每个时间步，贪心搜索选择具有最高条件概率的词元：

如下图,假设输出中有四个词元“A”“B”“C”和“<eos>”。每个时间步下的四个数字分别表示在该时间步生成“A”“B”“C”和“<eos>”的条件概率。在每个时间步,贪心搜索选择具有最高条件概率的词元。因此,将在图9.8.1中预测输出序列“A”“B”“C”和“<eos>”。这个输出序列的条件概率是0.5x0.4x0.4x0.6=0.048

图1：

例2：在时间步2，选择具有第二高条件概率的词元“C”(而非最高条件概率的词元)：

与图1不同,在时间步2中,我们选择图2中的词元“C”它具有第二高的条件概率。由于时间步3所基于的时间步1和2处的输出子序列已从图1中的“A”和“B”改变为图9.8.2中的“A”和“C”，因此时间步3处的每个词元的条件概率也在图2中改变。假设我们在时间步3选择词元“B”，于是当前的时间步4基于前三个时间步的输出子序列“A”“C”和“B”为条件，这与图1中的“A”“B”和“C”不同。因此、在图2中的时间步4生成每个词元的条件概率也不同于图1中的条件概率。结果，图2中的输出序列“A”“C”“B”和“<eos>”的条件概率为0.5x0.3x0.6x0.6=0.054,这大于图1中的贪心搜索的条件概率。这个例子说明:贪心搜索获得的输出序列“A”“B”“C”和“<eos>不一定是最佳序列。

图2：

穷举搜索

基本思想：穷举地列举所有可能的输出序列及其条件概率，然后计算输出条件概率最高的一个。
穷举搜索效果：获得最优序列。
穷举搜索弊端：计算量O( $|y|^{{T}'}$ )可能高的惊人。
和贪心搜索比较：计算量远大于贪心搜索，但是精度更高。

束搜索（beam search）

优点：计算成本和精度介于贪心搜索和穷举搜索之间。
是贪心搜索的改进版本
基本思想：在时间步1，我们选择具有最高条件概率的k个词元。这k个词元将分别是k个候选输出序列的第一个词元。在随后的每个时间步，基于上一时间步的k个候选输出序列，我们将继续从k|)|个可能的选择中挑出具有最高条件概率的k个候选输出序列。（k:束宽（beam size)(超参数））
举例说明：
图3：束搜索过程(束宽:2，输出序列的最大长度:3)。候选输出序列是A、C、AB、CE、ABD和CED
图3演示了東搜索的过程。假设输出的词表只包含五个元素: =(A,B,C,D,E),其中有一个是“<eos>”设置束宽为2，输出序列的最大长度为3。在时间步1，假设具有最高条件概率P(yc)的词元是A和C。在时间步2，我们计算所有 $y_{2}$ ∈y为

从这十个值中选择最大的两个，比如P(A,B|c)和P(C,E|c)。然后在时间步3，我们计算所有 $y_{3}$ ∈y为:

从这十个值中选择最大的两个,即P(A,B,D|c)和P(C,E,D|c),我们会得到六个候选输出序列:(1)A;(2)
C;(3)A,B;(4)C,E;(5)A,B,D;(6)C,E,D。最后，基于这六个序列(例如，丢弃包括“<eos>”和之后的部分)，我们获得最终候选输出序列集合。然后我们选择其中条件概率乘积最高的序列作为输出序列:

其中L是最终候选序列的长度，a通常设置为0.75。因为一个较长的序列在(9.8.4)的求和中会有更多的对数项，因此分母中的L“用于惩罚长序列。
束搜索的计算量为O(k|y|IT')，这个结果介于贪心搜索和穷举搜索之间。实际上，贪心搜索可以看作一种束宽为1的特殊类型的束搜索。通过灵活地选择束宽，束搜索可以在正确率和计算代价之间进行权衡。