由于 Heisenberg 测不准原理,线性时频变换方法无法同时在时间和频率方向达到最佳的时频分布,窗函数和小波函数的选择也降低了各方法的自适应性。同样,二次型变换方法难以在去除交叉干扰项的同时保证较高的能量集中度。为了解决该问题,一系列将时频系数重排到信号能量分布的重心,致力于提高能量集中度的后处理方法被提出。首先,通过分析相位信息来聚集分散的时频能量,在此基础上重排方法被提出以改进线性时频变换,其原理下所示。
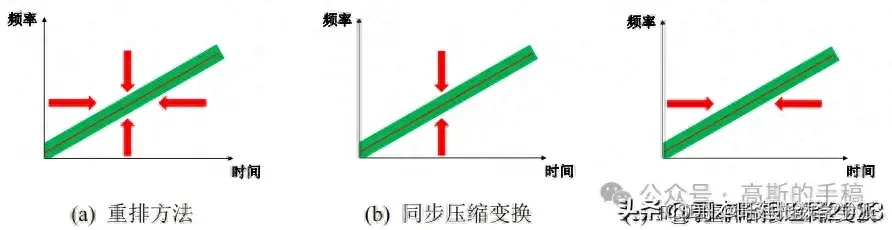
图中绿色矩形指时频系数分布位置,红色实线为理论瞬时频率,红色箭头为重排方向。该方法通过重新分配时频系数来提高时频分辨率,对微弱故障特征的提取至关重要。然而,重排方法在时间和频率两个方向重排时频系数丢失了信号的相位信息,故该方法不具备重构能力。在实际应用中,信号分析算法的可逆性是分离干扰能量的关键特性,因此多贝西提出一种基于小波变换的同步压缩变换,该方法将连续小波变换各个模态分量附近的能量聚集到瞬时频率算子,在提高时频分布可读性的同时保留信号重构的所需的信息。在此基础上,可以将该方法引入短时傅里叶变换和 S 变换的框架中,这些方法都取得了良好的效果,其适用性也得到了验证。然而,这些方法在处理强调频信号时效果不够理想,这导致其在现实应用难以处理如引力波、心电图等信号的分析。
近年来,随着同步压缩变换和时间重排同步压缩变换在各领域的成功应用,越来越多的学者以同步压缩技术为框架提出了大量改进方法。如针对强调频信号提出的解调变换,该方法使用解调算子对信号进行前处理,降低信号的非平稳度,最终提升同步压缩变换的处理效果。值得一提的是,解调算子的计算主要有两种方法:匹配解调算法和脊估计算法,前者适应性好但计算量偏大,后者计算成本更低但非常依赖脊估计算法。该方法的优势是可以与同步压缩变换结合使用,进一步提升时频分布的时频分辨率。此外,还有以大幅度提升时频分辨率为目标的多重同步压缩变换和时间重排多重同步压缩变换,为降低噪声影响提出的同步提取变换和瞬态提取变换,以及致力于提升算法泛化能力的自适应同步压缩变换等。
import numpy as np
from numpy import pi as pi
import seaborn as sns
import matplotlib.pyplot as plt
from src.utilities.utilstf import get_spectrogram
from mcsm_benchs.SignalBank import SignalBank
from mcsm_benchs.Benchmark import Benchmark
from src.methods.method_sstrd import NewMethod# np.random.seed(0)
# signal parameters
SNRin = 20
N = 2**10
# Nsub=N//2
sbank = SignalBank(N=N, return_signal=True)
tmin = sbank.tmin
tmax = sbank.tmax
s = sbank.signal_mc_multi_linear()
# s = sbank.signal_mc_crossing_chirps()
# s = sbank.signal_mc_synthetic_mixture()
s = sbank.signal_mc_synthetic_mixture_3()noise = np.random.randn(N,)
signal = Benchmark.sigmerge(s,noise,SNRin)Nfft = 2*N
S, F = get_spectrogram(s)
F = F[0:N+1]
methodml = NewMethod()
funa = methodml.method# signal_output = funa(signal,[],True,Pnei,M,L)
signal_output = funa(signal,)S_output, F_output = get_spectrogram(signal_output)
F_output = F_output[0:N+1]print(10*np.log10((np.sum(s[tmin:tmax]**2))/(np.sum((s[tmin:tmax]-signal_output[tmin:tmax])**2))))plt.figure()
plt.plot(s[tmin:tmax])
plt.plot(signal_output[tmin:tmax],'--')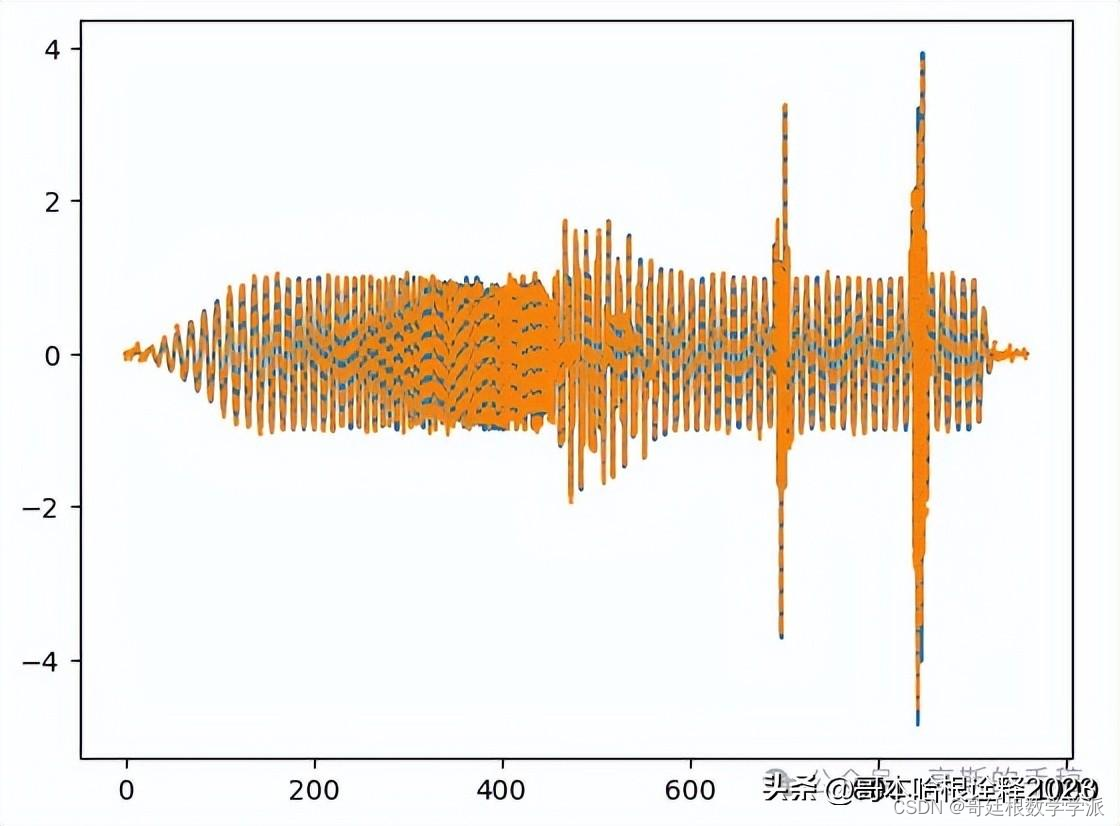
fig, ax = plt.subplots(1,3,figsize = (15,5))
ax[0].imshow(abs(F), origin='lower')#, cmap=cmocean.cm.deep)
ax[0].set_title('Input Signal')
ax[1].imshow(abs(F_output), origin='lower')#, cmap=cmocean.cm.deep)
ax[1].set_title('Output Signal')
ax[2].imshow(abs(F_output-F), origin='lower')#, cmap=cmocean.cm.deep)
ax[2].set_title('Difference')
plt.show()知乎学术咨询:
https://www.zhihu.com/consult/people/792359672131756032?isMe=1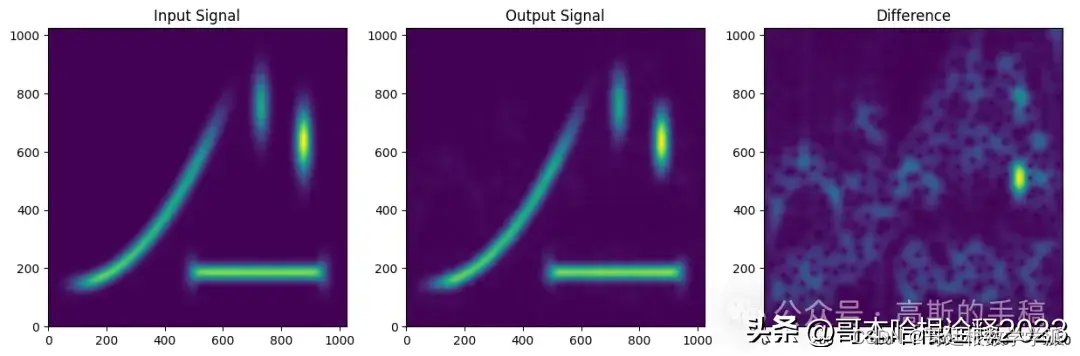
工学博士,担任《Mechanical System and Signal Processing》《中国电机工程学报》《控制与决策》等期刊审稿专家,擅长领域:现代信号处理,机器学习,深度学习,数字孪生,时间序列分析,设备缺陷检测、设备异常检测、设备智能故障诊断与健康管理PHM等。
