Bode曲线与Nyquist曲线的关系
Nyquist稳定性主要看Nyquist曲线绕（-1，j0）点的圈数N，与开环传递函数极点P是否相等。若相等Z=0则系统稳定，若不相等Z>0则系统不稳定。
Bode图中，，当
时，
；过（-1，j0）点时，
=-180°。
若包围（-1，j0）点，则需要看的是：L(w)>0，相角是否穿越-180°。
对数稳定判据
P-Z=N
N=(N+-N-)/2
N+：相位角度增加方向穿越-180°次数；
N-：相位角度减少方向穿越-180°次数。
当相角贴着-180°时，N+/N-=1/2，N+贴在-180°上方，N-贴在-180°下方。
若Z = 0，系统稳定，若Z>0，系统不稳定。
系统稳定程度研究
| 分析域 | 稳定边界 | 稳定程度 |
| 时域 | 虚轴 | 阻尼比 |
| 频域 | （-1，j0）点 | 到（-1，j0）点的距离，距离越远越稳定 稳定裕度 |
稳定裕度的定义与意义
表征闭环传递函数的稳定程度，直接表征了系统动态性能指标超调量、调节时间等的好坏。
截止频率:
，此时对应的相角裕度
：
；
相角交界频率:
，所对应的幅值裕度（开环模的倒数）h:
。
稳定裕度的计算
假设传递函数为，则幅值裕度和相角裕度可通过MATLAB绘制Nyquist曲线和Bode图得到，其代码实现如下：
sys=tf(100,conv([conv([1 0],[1 2])],[1 10]));
nyquist(sys);
v = [-1.5 0 -1.5 0.5];%限值坐标轴，全绘制出来，坐标轴过大，不好观察
axis(v);
margin(sys)
[h,gama,wg,wc]=margin(sys)
hdb = 20*log10(h)
wchz= wc/(2*pi)
wghz = wg/(2*pi)Nyquist曲线：
Bode图：
从绿色框线中可以得到：幅值裕度为GM=7.6dB，转化为数值 h = ，即幅值最大取2.398 ，则相角交界频率为：wg=4.47rad/s，转化为Hz，则为wg=4.47/(2*pi) = 0.7114Hz;
相角裕度：=19.9°，截止频率
。
由MATLAB程序也可求解得到：
一般要求：相角裕度>40°，幅值裕度>2（6DB）
相角裕度物理意义：系统在相角（时间延时）上距离临界稳定，还存在的储备量。
幅值裕度物理意义：系统在幅值（开环增益K）上距离临界稳定，还存在的储备量。
开环对数幅频特性分析系统性能
三频段理论
假设开环传递函数的对数频域特性曲线L(w)如图所示：
截止频率前后，中频段；第一个转折频率前，低频段；最后一个转折频率前，高频段。
1.
低频段渐近线与闭环系统稳态误差
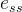的关系
低频段决定系统型别，决定闭环系统稳态误差。
-->
低频段型越高，bode图斜率越高、陡，则越小。
2.中频段特性与系统动态性能
的关系
一般地，()可以认为是中频段。
-20dB/dec 相角归宿-90°
-40dB/dec 相角归宿-180°
-60dB/dec 相角归宿-270°
-80dB/dec 相角归宿-360°；
斜率决定归宿，范围决定归宿的程度。相角最大的地方，是看谁的斜率最大且管辖范围宽。
以-20dB/dec 穿过0dB线，能达到比较好的闭环系统动态性能。
典型二阶欠阻尼系统
开环传递函数为：
相角裕度：，只和阻尼比有关，超调量
，也只和阻尼比相关，当系统相角裕度确定时，则系统的超调量也确定了。
查图法求解得到超调量，已知相角裕度，找到对应的阻尼比，进而得到系统超调量。
3.高频段特性与闭环系统抗干扰能力
Bode表征的是开环传递函数高频段的抗干扰能力，但同时也说明了闭环传递函数高频段的抗干扰能力。
高频段下降速度越快越好。
>10可认为是高频段。
通常，，因此在高频段，可以用开环频率特性直接表征闭环频率特性。
bode图上表现为截止频率以后，bode图中幅值曲线斜率越大，越陡，抗干扰能力越强。