网站建设什么公司好_黄页88网企业名录_长安seo排名优化培训_google海外版

布隆过滤器（Bloom Filter）是一种用于检验某个元素是否在集合中的概率性数据结构。它由布隆于1970年提出，具有很高的空间利用效率，但其结果存在一定的不确定性：要么说明该元素肯定不在集合中，要么说明该元素可能在集合中。因此，它经常用于需要快速检索但允许小概率误判的场景。

一、初始化

布隆过滤器本质上是一个位数组（bit array）和若干个独立的哈希函数。初始化时，位数组的所有元素都被设置为0。

二、插入

当向布隆过滤器中插入一个元素时，该元素会经过多个哈希函数，生成对应的多个位数组索引，并将这些索引位置上的值设为1。

三、查找

当查找一个元素是否存在时，可以采用相同的方式，经过多个哈希函数，生成对应的多个位数组索引，查询这些索引是否都为1，如果都为1则存在，如果不都为1那么则不存在。

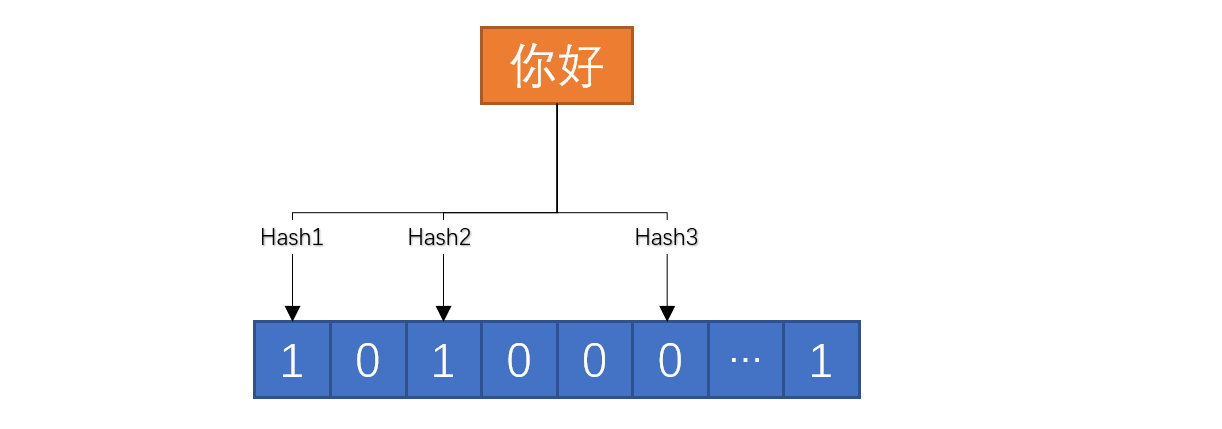
如上图所示，你好则不存在。

四、删除

布隆过滤器不支持删除操作，因为多个元素可能共享相同的位，删除某一个元素可能导致其他元素的哈希映射信息丢失。

五、如何选择哈希函数与位数组大小？

布隆过滤器存在一定的误判率（false positive），即查询时可能会得到“元素在集合中”，但实际上该元素并不在集合中。误判率取决于位数组的大小、哈希函数的数量以及插入的元素数量。为了在误判率与空间效率之间取得平衡，布隆过滤器设计中的两个关键参数是位数组大小（m）和哈希函数数量（k）。

• 位数组大小（m）：位数组越大，冲突的概率越低，误判率越小。但过大的位数组会增加存储空间开销。

• 哈希函数数量（k）：哈希函数数量的选择需要根据集合的大小（n）和位数组的大小（m）来确定。通常的选择是根据以下公式得出：
  $$k=\frac{m}{n}\ln 2$$
  这个公式能最小化误判率，确保最优的哈希函数数量。

六、应用场景

缓存系统：在大型缓存系统中，布隆过滤器可用于快速判断某个元素是否存在于缓存中，避免不必要的I/O操作。假设布隆过滤器判断某元素不在缓存中，那么直接请求数据库即可；如果布隆过滤器判断某元素可能在缓存中，再进行更精确的查找。

数据库去重：布隆过滤器可以用于判定一个元素是否已经在数据库中存在，从而避免重复插入。由于布隆过滤器的空间效率高，它适用于需要快速去重的场景，例如网页爬虫中去重URL。

网络黑名单过滤：布隆过滤器可以用于存储恶意IP地址或域名，通过快速查询判断某IP是否在黑名单中。

区块链和加密货币：布隆过滤器被广泛应用于区块链技术中，用于轻量级节点快速检测是否包含与其相关的交易数据。