目录
一、快速排序(非递归)
1.原理
2.实现
2.1 stack
2.2 partition(array,left,right)
2.3 pivot - 1 > left
二、归并排序(非递归)
1.原理
2.实现
2.1 gap
2.1.1 i += 2*gap
2.1.2 gap *= 2
2.1.3 gap < array.length
2.2 left、mid、right
2.2.1 left = i
2.2.2 mid >= array.length
前言:
在看快速排序的非递归实现之前,可以先看看快速排序用递归实现的版本:【算法】快速排序(递归实现),里面有详细介绍下面讲到的基准排序,基准排序是快速排序实现的基础,最好先去了解下再往下看
递归实现归并排序的也献上:【算法】归并排序(递归实现)
一、快速排序(非递归)
1.原理
- 在每一个待排元素所确定在的待排序区间内把待排序元素用基准排序一个个排好,等到把所有待排序区间对应的一个个待排序元素都排好后,整个数组就排好了
(在区间内进行基准排序时,默认以区间第一个元素为待排序元素)
用基准排序把每一个元素在对应已知的待排序范围排好,因为每排好一个元素,此元素排序位置确定且其排出的左小右大性质能缩小剩余的元素的待排序范围区域,所以每当一个元素排好后,其余元素对应的已知待排序范围就会发生变化,所以元素所在的待排序区域是经过动态变化来的
2.实现
public static void quickSortNonR(int[] array) {Stack<Integer> stack = new Stack<>();//2.1int left = 0;int right = array.length-1;int piovt = partition(array,left,right);//2.2if(piovt - 1 > left) {//2.3stack.push(left);stack.push(piovt-1);}if(piovt + 1 < right) {stack.push(piovt+1);stack.push(right);}while (!stack.isEmpty()) {right = stack.pop();left = stack.pop();piovt = partition(array,left,right);if(piovt - 1 > left) {stack.push(left);stack.push(piovt-1);}if(piovt + 1 < right) {stack.push(piovt+1);stack.push(right);}}}//2.2基准排序挖坑法实现:private static int partition(int[] array,int left,int right) {int key = array[left];while (left < right) {while (left < right && array[right] >= key) {right--;}//right下标元素一定比key小array[left] = array[right];while (left < right && array[left] <= key) {left++;}//left下标元素一定比key大array[right] = array[left];}array[left] = key;return left;}2.1 stack
利用栈的动态进出存储删取管理这些动态区间
2.2 partition(array,left,right)
partition方法是默认拿待排序区间的第一个元素为基准完成该元素在待排序区间内排好的
2.3 pivot - 1 > left
说明剩下的左边的待排序区域至少有两个元素,还是需要去进行基准排序的
二、归并排序(非递归)
1.原理
一轮轮去有序数组gap的两两合并,去合并的有序数组单位会越来越大,直到最后一次两两合并后成的是整体数组的一个有序数组,数组就整体排好序了
2.实现
public static void mergeSortNor(int[] array) {int gap = 1;//2.1while (gap < array.length) {//2.1.3for (int i = 0; i < array.length; i += 2*gap) {//2.1.1int left = i;//2.2.1int mid =left+gap-1;int right = mid+gap;if(mid >= array.length) {//2.2.2mid = array.length-1;}if(right >= array.length) {right = array.length-1;}merge(array,left,right,mid);}gap *= 2;//2.1.2}}private static void merge(int[] array, int left, int right, int mid) {int s1 = left;int s2 = mid+1;int[] tmpArr = new int[right-left+1];int k = 0;//证明两个区间都同时有数据的while (s1 <= mid && s2 <= right) {if(array[s2] <= array[s1]) {tmpArr[k++] = array[s2++];}else {tmpArr[k++] = array[s1++];}}while (s1 <= mid) {tmpArr[k++] = array[s1++];}while (s2 <= right) {tmpArr[k++] = array[s2++];}//tmpArr里面一定是这个区间内有序的数据了for (int i = 0; i < tmpArr.length; i++) {array[i+left] = tmpArr[i];}}2.1 gap
每轮去两两合并的单有序数组的元素个数,最开始的单位有序数组长度是1
2.1.1 i += 2*gap
一轮中往后继续去合并下一对的两gap有序数组
2.1.2 gap *= 2
一轮全部两两合并完后gap单位有序数组长度已翻倍
2.1.3 gap < array.length
gap >= array.length时,继续去有序数组合并也都只有一个靠前的左数组(整体数组),去合并也是没有变化了,且其实在gap >= array.length之前就一定有最后一次的两两合并成整体有序数组的了
2.2 left、mid、right
- [left,mid] —> 两合并数组中靠前的gap长度有序数组
- (mid,right] —> 两合并数组中靠后的gap长度有序数组
2.2.1 left = i
i < array.length,再进来的left是一定是left < array.length的
2.2.2 mid >= array.length
- 如果mid < array.length 但 right >= array.length:
左右两数组靠前的正常满足gap长度,靠后的不足gap长度,merge合并时也是正常合并
- 如果mid >= array.length - 1:
只有一个靠前的左数组,merge合并后还是它没变的左数组
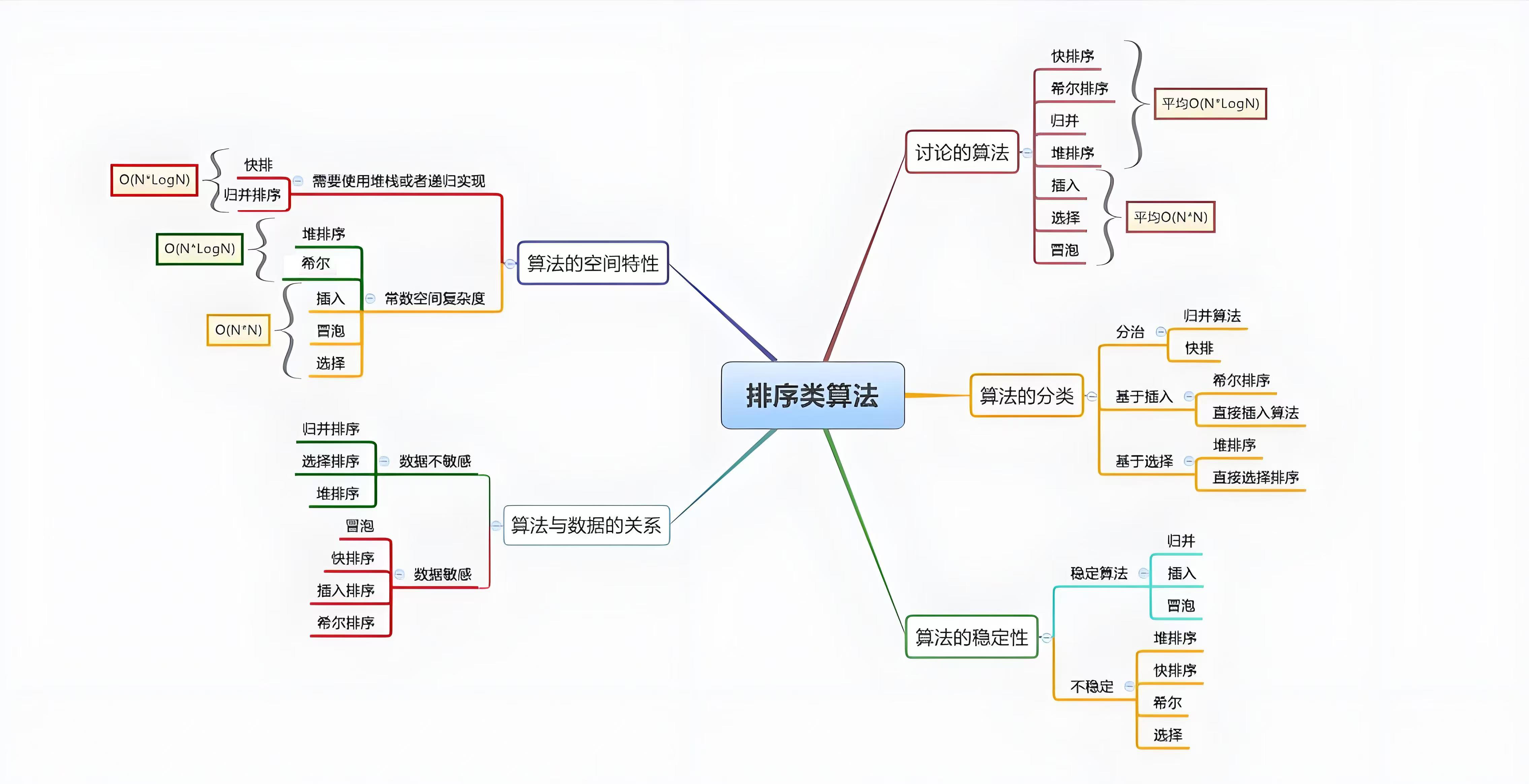
三、排序总结