简介与安装
PyTorch 是一个开源的 Python 机器学习库,基于 Torch 库,底层由C++实现,应用于人工智能领域,如计算机视觉和自然语言处理。
PyTorch 最初由 Meta Platforms 的人工智能研究团队开发,现在属 于Linux 基金会的一部分。
PyTorch 特性
-
动态计算图: PyTorch 的计算图是动态的,在执行时构建计算图,这意味着在每次计算时,图都会根据输入数据的形状自动变化。这为实验和调试提供了极大的灵活性,因为开发者可以逐行执行代码,查看中间结果。
-
张量计算: PyTorch 中的核心数据结构是
张量(Tensor),它是一个多维矩阵,可以在 CPU 或 GPU 上高效地进行计算。 -
自动微分求导: PyTorch 的自动微分系统允许开发者轻松地计算梯度,这对于训练深度学习模型至关重要。它通过反向传播算法自动计算出损失函数对模型参数的梯度。
-
丰富的 API: PyTorch 提供了大量的预定义层、损失函数和优化算法,这些都是构建深度学习模型的常用组件。
TensorFlow 和 PyTorch 的对比
| 对比维度 | TensorFlow | PyTorch |
|---|---|---|
| 开发团队 | Meta (Facebook) | |
| 设计理念 | 静态计算图(早期需先定义图,后执行) | 动态计算图(即时执行,更灵活) |
| 易用性 | 学习曲线陡峭,API 较复杂 | 接口简洁,Python 风格,更易调试 |
| 调试支持 | 需依赖 tf.debugging 工具 | 直接使用 Python 原生调试工具(如 pdb) |
| 部署能力 | 工业级部署成熟(TF Serving、TFLite) | 部署生态逐渐完善(TorchScript、ONNX) |
| 社区生态 | 企业用户多(Google、AWS 支持) | 学术界主导,研究论文实现更快速 |
| 移动端支持 | 强(TFLite 轻量化) | 较弱(依赖第三方工具转换) |
| 分布式训练 | 内置 tf.distribute(支持 TPU) | 依赖 torch.distributed(灵活性高) |
| 可视化工具 | TensorBoard(功能全面) | TensorBoard 或 Weights & Biases |
| 典型应用场景 | 生产环境、大型模型部署 | 研究原型开发、快速实验 |
| 代表项目 | Google BERT、DeepMind AlphaFold | OpenAI GPT、Stable Diffusion |
安装
在 Mac M3(Apple Silicon) 上安装 PyTorch,官方已提供原生 MPS(Metal Performance Shaders) 支持,可加速 GPU 计算。
pip install torch torchvision torchaudio
验证安装和 MPS 支持

使用 MPS 加速
在代码中显式指定设备为 mps:
device = torch.device("mps" if torch.backends.mps.is_available() else "cpu")
x = torch.randn(1000, 1000).to(device) # 数据转移到 MPS 设备
基础
训练过程
-
前向传播: 在前向传播阶段,输入数据通过网络层传递,每层应用权重和激活函数,直到产生输出。 -
计算损失: 根据网络的输出和真实标签,计算损失函数的值。 -
反向传播: 反向传播利用自动求导技术计算损失函数关于每个参数的梯度。 -
参数更新: 使用优化器根据梯度更新网络的权重和偏置。 -
迭代: 重复上述过程,直到模型在训练数据上的性能达到满意的水平。
数据类型
在 PyTorch 中,基础数据类型(dtype) 决定了张量(Tensor)中元素的存储方式和计算行为。以下是 PyTorch 支持的主要数据类型及其分类:
-
浮点类型(Float
数据类型 说明 适用场景 torch.float32(或torch.float)32 位单精度浮点数 通用计算(CPU/GPU) torch.float64(或torch.double)64 位双精度浮点数 高精度计算(科学计算) torch.float16(或torch.half)16 位半精度浮点数 GPU 加速(节省显存) torch.bfloat1616 位脑浮点数(保留指数位) TPU/部分 GPU 训练(如 A100) -
整数类型(Integer)
数据类型 说明 范围 torch.int88 位有符号整数 [-128, 127] torch.uint88 位无符号整数 [0, 255] torch.int16(或torch.short)16 位有符号整数 [-32768, 32767] torch.int32(或torch.int)32 位有符号整数 [-2^31, 2^31-1] torch.int64(或torch.long)64 位有符号整数 [-2^63, 2^63-1] -
布尔类型(Boolean)
数据类型 说明 torch.bool布尔值(True/False) -
复数类型(Complex)
数据类型 说明 torch.complex6464 位复数(32 位实部+虚部) torch.complex128128 位复数(64 位实部+虚部)
常用操作示例
-
指定数据类型创建张量
import torch# 创建指定类型的张量 x_float32 = torch.tensor([1.0, 2.0], dtype=torch.float32) x_int64 = torch.tensor([1, 2], dtype=torch.int64) x_bool = torch.tensor([True, False], dtype=torch.bool) -
转换数据类型
x = torch.tensor([1, 2], dtype=torch.int32) x_float = x.float() # 转换为 float32 x_double = x.double() # 转换为 float64 -
检查数据类型
print(x.dtype) # 输出: torch.int32
张量(Tensor)
张量(Tensor)是 PyTorch 中的核心数据结构,用于存储和操作多维数组。
张量可以视为一个多维数组,支持加速计算的操作。
在 PyTorch 中,张量的概念类似于 NumPy 中的数组,但是 PyTorch 的张量可以运行在不同的设备上,比如 CPU 和 GPU,这使得它们非常适合于进行大规模并行计算。
-
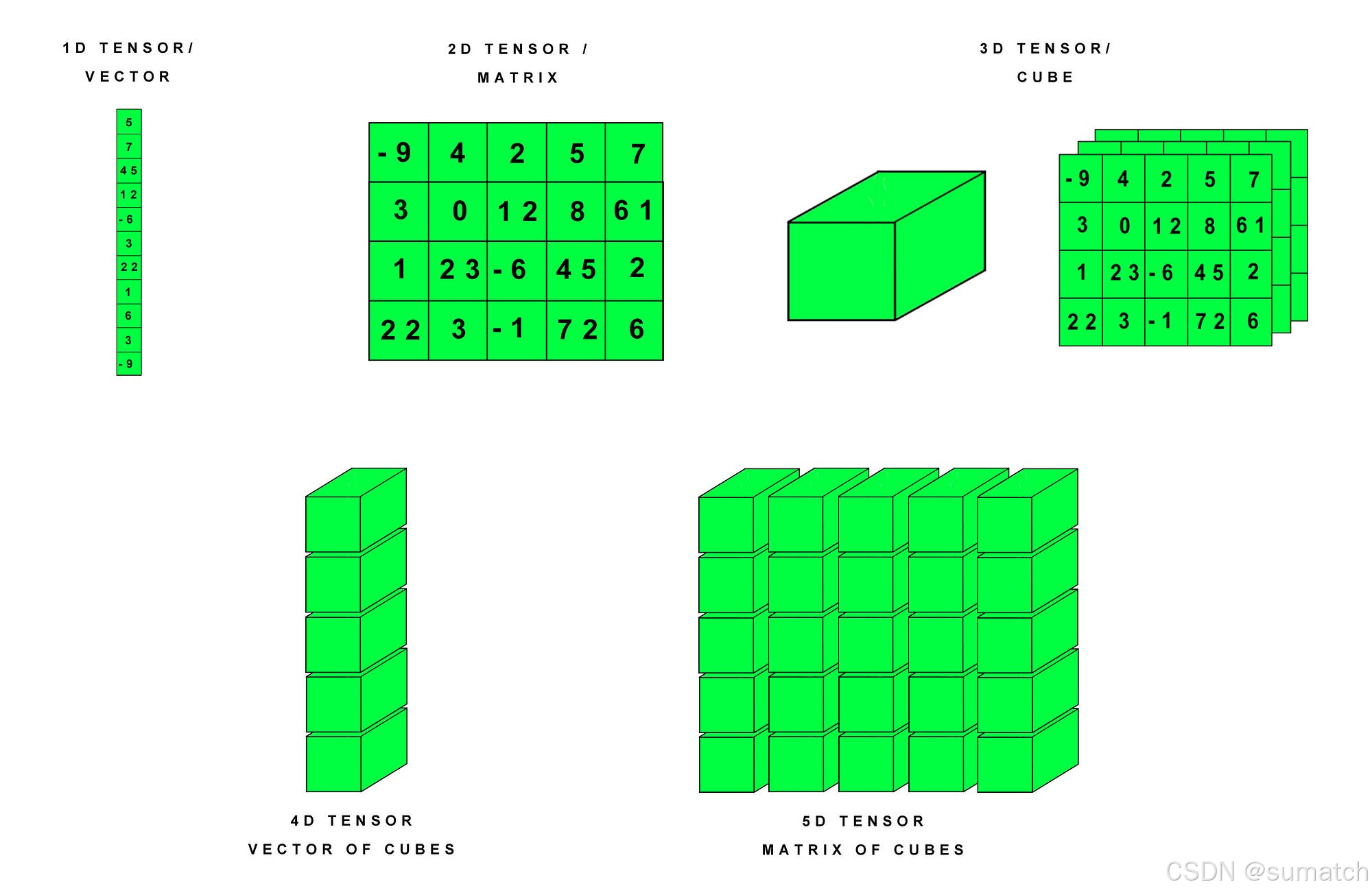
维度(Dimensionality):张量的维度指的是数据的多维数组结构。例如,一个标量(0维张量)是一个单独的数字,一个向量(1维张量)是一个一维数组,一个矩阵(2维张量)是一个二维数组,以此类推。 -
形状(Shape):张量的形状是指每个维度上的大小。例如,一个形状为 (3, 4) 的张量意味着它有3行4列。 -
数据类型(Dtype):张量中的数据类型定义了存储每个元素所需的内存大小和解释方式。PyTorch支持多种数据类型,包括整数型(如torch.int8、torch.int32)、浮点型(如torch.float32、torch.float64)和布尔型(torch.bool)。
创建张量
从数据直接创建:
| 具体方法 | 语法示例 | 适用场景 |
|---|---|---|
| 从 Python 列表/NumPy 数组转换 | torch.tensor([[1, 2], [3, 4]]) | 需要精确控制初始数据时 |
| 从 NumPy 数组转换(共享内存) | torch.from_numpy(np_array) | 与 NumPy 交互时 |
初始化创建:
| 具体方法 | 语法示例 | 适用场景 |
|---|---|---|
| 全零张量 | torch.zeros(2, 3) | 初始化权重/占位符 |
| 全一张量 | torch.ones(2, 3) | 初始化固定值张量 |
| 单位矩阵 | torch.eye(3) | 线性代数运算 |
| 等差数列张量 | torch.arange(0, 10, 2) | 生成连续数值 |
| 均匀分布随机张量 | torch.rand(2, 3) | 初始化权重(范围 [0, 1)) |
| 正态分布随机张量 | torch.randn(2, 3) | 初始化权重(均值 0,方差 1) |
| 自定义范围随机整数 | torch.randint(0, 10, (2, 3)) | 生成离散随机值 |
特殊初始化:
| 具体方法 | 语法示例 | 适用场景 |
|---|---|---|
| 空张量(未初始化,值不确定) | torch.empty(2, 3) | 高性能场景(需立即覆盖数据时) |
| 与现有张量同形状 | torch.zeros_like(input_tensor) | 快速创建形状匹配的张量 |
| 复制现有张量(可改设备/数据类型) | torch.clone(input_tensor) | 深拷贝张量 |
高级创建:
| 具体方法 | 语法示例 | 适用场景 |
|---|---|---|
| 对角线张量 | torch.diag(torch.tensor([1, 2, 3])) | 构建对角矩阵 |
| 稀疏张量 | torch.sparse_coo_tensor(indices, values, size) | 处理稀疏数据 |
| 自定义数值填充 | torch.full((2, 3), fill_value=5) | 需要特定填充值 |
设备控制:
| 具体方法 | 语法示例 | 适用场景 |
|---|---|---|
| 直接在 GPU 上创建 | torch.tensor([1, 2], device='cuda') | GPU 加速计算 |
| 从 GPU 复制到 CPU | cpu_tensor = gpu_tensor.cpu() | 设备间数据传输 |
示例:
import torch
# 创建一个 2x3 的全 0 张量
a = torch.zeros(2, 3)
print(a)
# tensor([[0., 0., 0.],
# [0., 0., 0.]])# 创建一个 2x3 的全 1 张量
b = torch.ones(2, 3)
print(b)
# tensor([[1., 1., 1.],
# [1., 1., 1.]])# 创建一个 2x3 的随机数张量
c = torch.randn(2, 3)
print(c)
# tensor([[-0.9105, 0.2726, -1.2604],
# [ 1.4011, -0.5314, -0.7574]])# 从 NumPy 数组创建张量
import numpy as np
numpy_array = np.array([[1, 2], [3, 4]])
tensor_from_numpy = torch.from_numpy(numpy_array)
print(tensor_from_numpy)
# tensor([[1, 2],
# [3, 4]])# 在指定设备(CPU/GPU)上创建张量
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
d = torch.randn(2, 3, device=device)
print(d)
# tensor([[ 1.7682, -1.7740, -1.9805],
# [-1.1396, -0.6919, 0.3156]])
张量的属性

张量操作:

形状操作

import torch# 张量相加
e = torch.randn(2, 3)
f = torch.randn(2, 3)
print(e + f)# 逐元素乘法
print(e * f)# 张量的转置
g = torch.randn(3, 2)
print(g.t()) # 或者 g.transpose(0, 1)# 张量的形状
print(g.shape) # torch.Size([3, 2])
张量与设备
PyTorch 张量可以存在于不同的设备上,包括 CPU 和 GPU,你可以将张量移动到 GPU 上以加速计算:
if torch.cuda.is_available():tensor_gpu = tensor_from_list.to('cuda') # 将张量移动到GPU
梯度和自动微分
PyTorch 的张量支持自动微分,这是深度学习中的关键特性。当你创建一个需要梯度的张量时,PyTorch 可以自动计算其梯度:
import torch# 创建一个需要梯度的张量
tensor_requires_grad = torch.tensor([1.0], requires_grad=True)# 进行一些操作
tensor_result = tensor_requires_grad * 2# 反向传传播,计算梯度
tensor_result.backward()
print(tensor_requires_grad.grad) # tensor([2.])
打印原始张量的梯度值,结果是 [2.],这是因为:
- 计算过程是
y = 2x - 导数
dy/dx = 2 - 所以当
x=1.0时,梯度值为2
这段代码展示了 PyTorch 自动微分系统的核心功能,是神经网络训练中反向传播的基础。
自动求导
在深度学习中,自动求导主要用于两个方面:一是在训练神经网络时计算梯度,二是进行反向传播算法的实现。
动态图与静态图:
-
动态图(Dynamic Graph):在动态图中,计算图在运行时动态构建。每次执行操作时,计算图都会更新,这使得调试和修改模型变得更加容易。PyTorch使用的是动态图。
-
静态图(Static Graph):在静态图中,计算图在开始执行之前构建完成,并且不会改变。TensorFlow最初使用的是静态图,但后来也支持动态图。
PyTorch 提供了自动求导功能,通过 autograd 模块来自动计算梯度。
torch.Tensor 对象有一个 requires_grad 属性,用于指示是否需要计算该张量的梯度。
当你创建一个 requires_grad=True 的张量时,PyTorch 会自动跟踪所有对它的操作,以便在之后计算梯度。
import torch# 创建一个需要计算梯度的张量
x = torch.randn(2, 2, requires_grad=True)
print(x)
# tensor([[ 1.2989, 1.3075],
# [-0.3233, 0.4261]], requires_grad=True)# 执行某些操作
y = x + 2
# y = [[1.2989+2, 1.3075+2],
# [-0.3233+2, 0.4261+2]]
# = [[3.2989, 3.3075],
# [1.6767, 2.4261]]z = y * y * 3
# z = [[3.2989²×3, 3.3075²×3],
# [1.6767²×3, 2.4261²×3]]
# = [[32.6438, 32.8187],
# [8.4324, 17.6527]]# z.mean()表示计算张量z中所有元素的平均值(算术平均数)
out = z.mean()
# out = (32.6438 + 32.8187 + 8.4324 + 17.6527) / 4
# = 91.5476 / 4
# ≈ 22.8869print(out)
# tensor(22.8894, grad_fn=<MeanBackward0>)
反向传播
在神经网络训练中,自动求导主要用于实现反向传播算法。
反向传播是一种通过计算损失函数关于网络参数的梯度来训练神经网络的方法。在每次迭代中,网络的前向传播会计算输出和损失,然后反向传播会计算损失关于每个参数的梯度,并使用这些梯度来更新参数。
一旦定义了计算图,可以通过 .backward() 方法来计算梯度。
x = torch.tensor([[1.2989, 1.3075],[-0.3233, 0.4261]], requires_grad=True)
y = x + 2
z = y * y * 3
out = z.mean()# 反向传播,计算梯度
out.backward()# 查看 x 的梯度
print(x.grad)
# tensor([[4.9483, 4.9612],
# [2.5150, 3.6392]])


前向传播与损失计算
import torch
import torch.nn as nn# 定义一个简单的全连接神经网络
class SimpleNN(nn.Module):def __init__(self):super(SimpleNN, self).__init__()self.fc1 = nn.Linear(2, 2) # 输入层到隐藏层self.fc2 = nn.Linear(2, 1) # 隐藏层到输出层def forward(self, x):x = torch.relu(self.fc1(x)) # ReLU 激活函数x = self.fc2(x)return x# 创建网络实例
model = SimpleNN()# 随机输入
x = torch.randn(1, 2)# 前向传播
output = model(x) # 模型预测值
print(output)
# tensor([[0.6781]], grad_fn=<AddmmBackward0>)# 定义损失函数(例如均方误差 MSE = 1/n * Σ(y_pred - y_true)^2)
criterion = nn.MSELoss()target = torch.randn(1, 1) # 目标值
print(target)
# tensor([[-0.4049]])# 计算损失
loss = criterion(output, target)
# loss = (output - target)^2
# = (0.6781 - (-0.4049))^2
# = (1.0830)^2
# ≈ 1.1730print(loss)
# tensor(1.1730, grad_fn=<MseLossBackward0>)
优化器(Optimizers)
优化器是模型训练的"方向盘",负责高效、稳定地更新参数。
在 PyTorch 中,优化器(Optimizer) 是训练神经网络的核心组件,其作用是 通过反向传播计算出的梯度,动态调整模型参数(权重和偏置),以最小化损失函数。
-
核心作用
功能 说明 参数更新 根据梯度下降算法,自动调整模型参数( weight和bias)。学习率控制 通过设置学习率( lr),控制参数更新的步长(避免震荡或收敛过慢)。梯度处理 支持动量(Momentum)、自适应学习率等策略,加速收敛或避免局部最优。 批量处理 兼容不同批量大小(Batch Size),适应 SGD、Mini-batch GD 等训练方式。
-
优化器的工作流程
import torch.optim as optim# 定义模型和优化器 model = SimpleModel() # 假设有一个简单的模型 optimizer = optim.SGD(model.parameters(), lr=0.01) # 随机梯度下降for epoch in range(100):# 前向传播output = model(x)loss = criterion(output, target)# 反向传播optimizer.zero_grad() # 清空梯度(重要!)loss.backward() # 计算梯度# 参数更新optimizer.step() # 根据梯度更新参数关键步骤解释:
-
zero_grad()
• 清空参数的梯度缓存(避免梯度累加)。
• 如果不调用:每次迭代的梯度会与上一次叠加,导致参数更新错误。 -
backward()
• 自动计算所有可训练参数的梯度(存储在parameter.grad中)。 -
step()
• 根据优化器策略(如 SGD、Adam)更新参数。
-
-
常用优化器类型
优化器 特点 适用场景 SGD 基础随机梯度下降,可添加动量(Momentum)。 简单任务,需要精细调参时。 Adam 自适应学习率,结合动量(默认选择)。 大多数深度学习任务(推荐默认)。 RMSprop 自适应学习率,适合非平稳目标(如 RNN)。 循环神经网络或强化学习。 Adagrad 自适应学习率,但学习率会单调递减(可能过早停止)。 稀疏数据(如推荐系统)。 常用优化器定义
optimizer_adam = optim.Adam(model.parameters(), lr=0.001) optimizer_sgd = optim.SGD(model.parameters(), lr=0.01, momentum=0.9) optimizer_rmsprop = optim.RMSprop(model.parameters(), lr=0.01, alpha=0.99) -
优化器的关键参数**
参数 说明 lr学习率(关键!过大导致震荡,过小收敛慢)。 momentum动量因子(加速收敛,减少震荡)。 weight_decayL2 正则化系数(防止过拟合)。 betasAdam 优化器的超参数(默认 (0.9, 0.999))。学习率设置技巧:
• 初始值:通常尝试
0.001(Adam)或0.01(SGD)。
• 动态调整:使用lr_scheduler动态调整学习率:scheduler = optim.lr_scheduler.StepLR(optimizer, step_size=30, gamma=0.1) scheduler.step() # 每隔 step_size 轮,学习率乘以 gamma
训练模型
训练模型是机器学习和深度学习中的核心过程,旨在通过大量数据学习模型参数,以便模型能够对新的、未见过的数据做出准确的预测。
训练模型通常包括以下几个步骤:
-
数据准备:
- 收集和处理数据,包括清洗、标准化和归一化。
- 将数据分为训练集、验证集和测试集。
-
定义模型:
- 选择模型架构,例如决策树、神经网络等。
- 初始化模型参数(权重和偏置)。
-
选择损失函数:
- 根据任务类型(如分类、回归)选择合适的损失函数。
-
选择优化器:
- 选择一个优化算法,如SGD、Adam等,来更新模型参数。
-
前向传播:
- 在每次迭代中,将输入数据通过模型传递,计算预测输出。
-
计算损失:
- 使用损失函数评估预测输出与真实标签之间的差异。
-
反向传播:
- 利用自动求导计算损失相对于模型参数的梯度。
-
参数更新:
- 根据计算出的梯度和优化器的策略更新模型参数。
-
迭代优化:
- 重复步骤5-8,直到模型在验证集上的性能不再提升或达到预定的迭代次数。
-
评估和测试:
使用测试集评估模型的最终性能,确保模型没有过拟合。
-
模型调优:
根据模型在测试集上的表现进行调参,如改变学习率、增加正则化等。
-
部署模型:
将训练好的模型部署到生产环境中,用于实际的预测任务。
import torch
import torch.nn as nn
import torch.optim as optim# 1. 定义一个简单的神经网络模型
class SimpleNN(nn.Module):def __init__(self):super(SimpleNN, self).__init__()self.fc1 = nn.Linear(2, 2) # 输入层到隐藏层self.fc2 = nn.Linear(2, 1) # 隐藏层到输出层def forward(self, x):x = torch.relu(self.fc1(x)) # ReLU 激活函数x = self.fc2(x)return x# 2. 创建模型实例
model = SimpleNN()# 3. 定义损失函数和优化器
criterion = nn.MSELoss() # 均方误差损失函数
optimizer = optim.Adam(model.parameters(), lr=0.001) # Adam 优化器# 4. 假设我们有训练数据 X 和 Y
X = torch.randn(10, 2) # 10 个样本,2 个特征
Y = torch.randn(10, 1) # 10 个目标值# 5. 训练循环
for epoch in range(100): # 训练 100 轮optimizer.zero_grad() # 清空之前的梯度output = model(X) # 前向传播loss = criterion(output, Y) # 计算损失loss.backward() # 反向传播optimizer.step() # 更新参数# 每 10 轮输出一次损失if (epoch + 1) % 10 == 0:print(f'Epoch [{epoch + 1}/100], Loss: {loss.item():.4f}')# Epoch[10 / 100], Loss: 0.8042# Epoch[20 / 100], Loss: 0.7891# Epoch[30 / 100], Loss: 0.7745# Epoch[40 / 100], Loss: 0.7606# Epoch[50 / 100], Loss: 0.7474# Epoch[60 / 100], Loss: 0.7348# Epoch[70 / 100], Loss: 0.7226# Epoch[80 / 100], Loss: 0.7108# Epoch[90 / 100], Loss: 0.6994# Epoch[100 / 100], Loss: 0.6885
在每 10 轮,程序会输出当前的损失值,帮助我们跟踪模型的训练进度。随着训练的进行,损失值应该会逐渐降低,表示模型在不断学习并优化其参数。
训练模型是一个迭代的过程,需要不断地调整和优化,直到达到满意的性能。这个过程涉及到大量的实验和调优,目的是使模型在新的、未见过的数据上也能有良好的泛化能力。
设备
PyTorch 允许你将模型和数据移动到 GPU 上进行加速。
使用 torch.device 来指定计算设备。
将模型和数据移至 GPU:
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")# 将模型移动到设备
model.to(device)# 将数据移动到设备
X = X.to(device)
Y = Y.to(device)
在训练过程中,所有张量和模型都应该移到同一个设备上(要么都在 CPU 上,要么都在 GPU 上)。
梯度消失 / 爆炸
梯度消失(Gradient Vanishing)和梯度爆炸(Gradient Explosion)是深度神经网络(尤其是循环神经网络 RNN)训练过程中常见的两类问题,它们与反向传播时的梯度传递机制密切相关。
-
梯度消失(Gradient Vanishing)
问题描述
在反向传播时,梯度(即损失函数对参数的偏导数)随着网络层数的增加 指数级减小,导致浅层网络的参数几乎无法更新,模型无法学习到远距离依赖关系。原因
- 链式法则的连乘效应:梯度通过反向传播逐层传递时,需连续乘以权重矩阵和激活函数的导数。若这些值 ( \ll 1 ),连乘后梯度趋近于零。
- 激活函数的选择:如 Sigmoid 或 Tanh 的导数范围在 ( (0, 1] ),连乘后梯度迅速缩小。
影响
RNN 难以捕捉长期依赖(例如预测句子开头对结尾的影响)。
深层网络的前几层参数几乎不更新,训练停滞。典型案例
传统 RNN 在处理长序列时,梯度因时间步的连乘而消失。解决方案
-
使用 LSTM/GRU:门控机制保留长期记忆,避免梯度连乘。
-
残差连接(ResNet):通过跳跃连接绕过深层,直接传递梯度。
-
激活函数替换:如 ReLU 及其变体(LeakyReLU)的导数为常数(正区间)。
-
梯度爆炸(Gradient Explosion)
问题描述
梯度在反向传播过程中 指数级增大,导致参数更新幅度过大,模型无法收敛(甚至出现数值溢出 NaN)。原因
- 权重矩阵的范数过大:若权重矩阵的特征值 ( \gg 1 ),连乘后梯度急剧增长。
- 缺乏梯度裁剪:未对梯度进行约束。
影响
- 参数剧烈震荡,损失函数值剧烈波动。
- 数值不稳定,可能出现 NaN。
典型案例
深层前馈网络或未规范化的 RNN 中常见。解决方案
- 权重正则化:L2 正则化约束权重范数。
- 梯度裁剪:设定阈值,限制梯度最大值,强制梯度不超过阈值(如
torch.nn.utils.clip_grad_norm_)。
-
两类问题的对比
特征 梯度消失 梯度爆炸 梯度变化 趋近于零 趋近于无穷大 主要成因 连乘小数(如激活函数导数) 连乘大权重矩阵 网络类型 常见于 RNN/深层网络 深层网络或大权重 RNN 表现 参数更新几乎停止 参数剧烈震荡,NaN 错误
- 数学直观*

-
代码示例(梯度裁剪)
import torch import torch.nn as nnmodel = nn.LSTM(input_size=10, hidden_size=20, num_layers=2) optimizer = torch.optim.Adam(model.parameters(), lr=0.01)# 训练循环中 loss.backward() torch.nn.utils.clip_grad_norm_(model.parameters(), max_norm=1.0) # 裁剪梯度 optimizer.step()
总结
梯度消失和爆炸本质是反向传播中梯度链式法则的副作用,通过结构设计(如 LSTM)、正则化和工程技巧(如裁剪)可有效缓解。理解这两类问题对设计稳定训练的深度模型至关重要。
神经网络基础
神经网络是一种模仿人脑神经元连接的计算模型,由多层节点(神经元)组成,用于学习数据之间的复杂模式和关系。
神经网络通过调整神经元之间的连接权重来优化预测结果,这一过程涉及前向传播、损失计算、反向传播和参数更新。
神经网络的类型包括前馈神经网络、卷积神经网络(CNN)、循环神经网络(RNN)和长短期记忆网络(LSTM),它们在图像识别、语音处理、自然语言处理等多个领域都有广泛应用。
PyTorch 提供了一个非常方便的接口来构建神经网络模型,即 torch.nn.Module。
我们可以继承 nn.Module 类并定义自己的网络层。
创建一个简单的神经网络:
import torch
import torch.nn as nn# 定义一个简单的全连接神经网络
class SimpleNN(nn.Module):def __init__(self):super(SimpleNN, self).__init__()self.fc1 = nn.Linear(2, 2) # 输入层到隐藏层self.fc2 = nn.Linear(2, 1) # 隐藏层到输出层def forward(self, x):x = torch.relu(self.fc1(x)) # ReLU 激活函数x = self.fc2(x)return x# 创建网络实例
model = SimpleNN()# 打印模型结构
print(model)
# SimpleNN(
# (fc1): Linear(in_features=2, out_features=2, bias=True)
# (fc2): Linear(in_features=2, out_features=1, bias=True)
# )
神经元(Neuron)
神经元是神经网络的基本单元,它接收输入信号,通过加权求和后与偏置(bias)相加,然后通过激活函数处理以产生输出。

神经元的权重和偏置是网络学习过程中需要调整的参数。

层(Layer)
输入层和输出层之间的层被称为隐藏层,层与层之间的连接密度和类型构成了网络的配置。
神经网络由多个层组成,包括:
- 输入层(Input Layer):接收原始输入数据。
- 隐藏层(Hidden Layer):对输入数据进行处理,可以有多个隐藏层。
- 输出层(Output Layer):产生最终的输出结果。
典型的神经网络架构:

前馈神经网络(FNN)
前馈神经网络(Feedforward Neural Network,FNN)是神经网络家族中的基本单元。
前馈神经网络特点是数据从输入层开始,经过一个或多个隐藏层,最后到达输出层,全过程没有循环或反馈。
前馈神经网络的基本结构:
-
输入层: 数据进入网络的入口点。输入层的每个节点代表一个输入特征。
-
隐藏层:一个或多个层,用于捕获数据的非线性特征。每个隐藏层由多个神经元组成,每个神经元通过激活函数增加非线性能力。
-
输出层:输出网络的预测结果。节点数和问题类型相关,例如分类问题的输出节点数等于类别数。
-
连接权重与偏置:每个神经元的输入通过权重进行加权求和,并加上偏置值,然后通过激活函数传递。

卷积神经网络(CNN)
CNN 是计算机视觉任务(如图像分类、目标检测和分割)的核心技术。
下面这张图展示了一个典型的卷积神经网络(CNN)的结构和工作流程,用于图像识别任务。

在图中,CNN 的输出层给出了三个类别的概率:Donald(0.2)、Goofy(0.1)和Tweety(0.7),这表明网络认为输入图像最有可能是 Tweety。
以下是各个部分的简要说明:
-
输入图像(Input Image):网络接收的原始图像数据。 -
卷积(Convolution):使用卷积核(Kernel)在输入图像上滑动,提取特征,生成特征图(Feature Maps)。 -
池化(Pooling):通常在卷积层之后,通过最大池化或平均池化减少特征图的尺寸,同时保留重要特征,生成池化特征图(Pooled Feature Maps)。 -
特征提取(Feature Extraction):通过多个卷积和池化层的组合,逐步提取图像的高级特征。 -
展平层(Flatten Layer):将多维的特征图转换为一维向量,以便输入到全连接层。 -
全连接层(Fully Connected Layer):类似于传统的神经网络层,用于将提取的特征映射到输出类别。 -
分类(Classification):网络的输出层,根据全连接层的输出进行分类。 -
概率分布(Probabilistic Distribution):输出层给出每个类别的概率,表示输入图像属于各个类别的可能性。
卷积神经网络的基本结构
-
输入层(Input Layer)接收原始图像数据,图像通常被表示为一个三维数组,其中两个维度代表图像的宽度和高度,第三个维度代表颜色通道(例如,RGB图像有三个通道)。
-
卷积层(Convolutional Layer)用卷积核提取局部特征,如边缘、纹理等。
公式:

应用一组可学习的滤波器(或卷积核)在输入图像上进行卷积操作,以提取局部特征。每个滤波器在输入图像上滑动,生成一个特征图(Feature Map),表示滤波器在不同位置的激活。
卷积层可以有多个滤波器,每个滤波器生成一个特征图,所有特征图组成一个特征图集合。
-
激活函数(Activation Function)通常在卷积层之后应用非线性激活函数,如 ReLU(Rectified Linear Unit),以引入非线性特性,使网络能够学习更复杂的模式。
ReLU 函数定义为 :
f(x)=max(0,x),即如果输入小于 0 则输出 0,否则输出输入值。 -
池化层(Pooling Layer)用于降低特征图的空间维度,减少计算量和参数数量,同时保留最重要的特征信息。
最常见的池化操作是最大池化(Max Pooling)和平均池化(Average Pooling)。
最大池化选择区域内的最大值,而平均池化计算区域内的平均值。 -
归一化层(Normalization Layer,可选)例如,局部响应归一化(Local Response Normalization, LRN)或批归一化(Batch Normalization)。
这些层有助于加速训练过程,提高模型的稳定性。 -
全连接层(Fully Connected Layer)在 CNN 的末端,将前面层提取的特征图展平(Flatten)成一维向量,然后输入到全连接层。
全连接层的每个神经元都与前一层的所有神经元相连,用于综合特征并进行最终的分类或回归。 -
输出层(Output Layer)根据任务的不同,输出层可以有不同的形式。
对于分类任务,通常使用 Softmax 函数将输出转换为概率分布,表示输入属于各个类别的概率。
-
损失函数(Loss Function)用于衡量模型预测与真实标签之间的差异。
常见的损失函数包括交叉熵损失(Cross-Entropy Loss)用于多分类任务,均方误差(Mean Squared Error, MSE)用于回归任务。
-
优化器(Optimizer)用于根据损失函数的梯度更新网络的权重。常见的优化器包括随机梯度下降(SGD)、Adam、RMSprop等。
-
正则化(Regularization,可选)包括 Dropout、L1/L2 正则化等技术,用于防止模型过拟合。
全连接神经网络 和 卷积神经网络区别
由下面两张图得知:
- 全连接神经网络需要 16*9=144 次乘积运算,共144个参数
- CNN 需要36次乘积运算,共4个参数


循环神经网络(RNN)
循环神经网络(Recurrent Neural Network, RNN)是一类专门处理序列数据的神经网络,能够捕获输入数据中时间或顺序信息的依赖关系。
RNN 的特别之处在于它具有"记忆能力",可以在网络的隐藏状态中保存之前时间步的信息。
循环神经网络用于处理随时间变化的数据模式。
在 RNN 中,相同的层被用来接收输入参数,并在指定的神经网络中显示输出参数。

循环神经网络(Recurrent Neural Networks, RNN)是一类神经网络架构,专门用于处理序列数据,能够捕捉时间序列或有序数据的动态信息,能够处理序列数据,如文本、时间序列或音频。
RNN 的关键特性是其能够保持隐状态(hidden state),使得网络能够记住先前时间步的信息,这对于处理序列数据至关重要。
RNN 的基本结构
在传统的前馈神经网络(Feedforward Neural Network)中,数据是从输入层流向输出层的,而在 RNN 中,数据不仅沿着网络层级流动,还会在每个时间步骤上传播到当前的隐层状态,从而将之前的信息传递到下一个时间步骤。
隐状态(Hidden State): RNN 通过隐状态来记住序列中的信息。
隐状态是通过上一时间步的隐状态和当前输入共同计算得到的。
公式:

输出(Output): RNN 的输出不仅依赖当前的输入,还依赖于隐状态的历史信息。
公式:

RNN 如何处理序列数据
循环神经网络(RNN)在处理序列数据时的展开(unfold)视图如下:


RNN 5种结构

激活函数
激活函数决定了神经元是否应该被激活。它们是非线性函数,使得神经网络能够学习和执行更复杂的任务。常见的激活函数包括:
- Sigmoid:用于二分类问题,输出值在 0 和 1 之间。
- Tanh:输出值在 -1 和 1 之间,常用于输出层之前。
- ReLU(Rectified Linear Unit):目前最流行的激活函数之一,定义为 f(x) = max(0, x),有助于解决梯度消失问题。
- Softmax:常用于多分类问题的输出层,将输出转换为概率分布。
import torch.nn.functional as F# ReLU 激活
output = F.relu(input_tensor)# Sigmoid 激活
output = torch.sigmoid(input_tensor)# Tanh 激活
output = torch.tanh(input_tensor)
损失函数
损失函数用于衡量模型的预测值与真实值之间的差异。
常见的损失函数包括:
- 均方误差(MSELoss):回归问题常用,计算输出与目标值的平方差。
- 交叉熵损失(CrossEntropyLoss):分类问题常用,计算输出和真实标签之间的交叉熵。
- BCEWithLogitsLoss:二分类问题,结合了 Sigmoid 激活和二元交叉熵损失。
# 均方误差损失
criterion = nn.MSELoss()# 交叉熵损失
criterion = nn.CrossEntropyLoss()# 二分类交叉熵损失
criterion = nn.BCEWithLogitsLoss()
LSTM
LSTM 是一种特殊的 循环神经网络(RNN),专门设计用于解决传统 RNN 的 长期依赖问题(即难以学习远距离信息依赖的问题)。
通过引入 门控机制,LSTM 能够选择性地记住或遗忘信息,从而有效捕捉时间序列中的长期模式。


import torch.nn as nn# 定义 LSTM 模型
class LSTMModel(nn.Module):def __init__(self, input_size, hidden_size, num_layers):super().__init__()self.lstm = nn.LSTM(input_size, hidden_size, num_layers, batch_first=True)self.fc = nn.Linear(hidden_size, 1) # 假设输出为1维def forward(self, x):out, _ = self.lstm(x) # out: [batch_size, seq_len, hidden_size]out = self.fc(out[:, -1, :]) # 取最后一个时间步的输出return out# 参数说明
# input_size: 输入特征维度(如词向量维度)
# hidden_size: 隐藏层维度
# num_layers: LSTM 层数
神经网络类型
- 前馈神经网络(Feedforward Neural Networks,
FNN):数据单向流动,从输入层到输出层,无反馈连接。 - 卷积神经网络(Convolutional Neural Networks,
CNN):适用于图像处理,使用卷积层提取空间特征。 - 循环神经网络(Recurrent Neural Networks,
RNN):适用于序列数据,如时间序列分析和自然语言处理,允许信息反馈循环。 - 长短期记忆网络(Long Short-Term Memory,
LSTM):一种特殊的 RNN,能够学习长期依赖关系。
Transformer
Transformer 模型是一种基于注意力机制的深度学习模型,最初由 Vaswani 等人在 2017 年的论文《Attention is All You Need》中提出。
Transformer 彻底改变了自然语言处理(NLP)领域,并逐渐扩展到计算机视觉(CV)等领域。
Transformer 的核心思想是完全摒弃传统的循环神经网络(RNN)结构,仅依赖注意力机制来处理序列数据,从而实现更高的并行性和更快的训练速度。
以下是 Transformer 架构图,左边为编码器,右边为解码器。

Transformer 模型由 编码器(Encoder) 和 解码器(Decoder) 两部分组成,每部分都由多层堆叠的相同模块构成。

编码器(Encoder)
编码器由 NN 层相同的模块堆叠而成,每层包含两个子层:
多头自注意力机制(Multi-Head Self-Attention):计算输入序列中每个词与其他词的相关性。前馈神经网络(Feed-Forward Neural Network):对每个词进行独立的非线性变换。
每个子层后面都接有 残差连接(Residual Connection) 和 层归一化(Layer Normalization)。
解码器(Decoder)
解码器也由 NN 层相同的模块堆叠而成,每层包含三个子层:
掩码多头自注意力机制(Masked Multi-Head Self-Attention):计算输出序列中每个词与前面词的相关性(使用掩码防止未来信息泄露)。编码器-解码器注意力机制(Encoder-Decoder Attention):计算输出序列与输入序列的相关性。前馈神经网络(Feed-Forward Neural Network):对每个词进行独立的非线性变换。
同样,每个子层后面都接有残差连接和层归一化。
在 Transformer 模型出现之前,NLP 领域的主流模型是基于 RNN 的架构,如长短期记忆网络(LSTM)和门控循环单元(GRU)。这些模型通过顺序处理输入数据来捕捉序列中的依赖关系,但存在以下问题:
-
梯度消失问题:长距离依赖关系难以捕捉。
-
顺序计算的局限性:无法充分利用现代硬件的并行计算能力,训练效率低下。
Transformer 通过引入自注意力机制解决了这些问题,允许模型同时处理整个输入序列,并动态地为序列中的每个位置分配不同的权重。
Transformer 的核心思想
-
自注意力机制(Self-Attention)
自注意力机制允许模型在处理序列时,动态地为每个位置分配不同的权重,从而捕捉序列中任意两个位置之间的依赖关系。
-
输入表示:输入序列中的每个词(或标记)通过词嵌入(Embedding)转换为向量表示。
-
注意力权重计算:通过计算查询(Query)、键(Key)和值(Value)之间的点积,得到每个词与其他词的相关性权重。
-
加权求和:使用注意力权重对值(Value)进行加权求和,得到每个词的上下文表示。
公式如下:

-
-
多头注意力(Multi-Head Attention)
为了捕捉更丰富的特征,Transformer 使用多头注意力机制。它将输入分成多个子空间,每个子空间独立计算注意力,最后将结果拼接起来。
多头注意力的优势:允许模型关注序列中不同的部分,例如语法结构、语义关系等。
并行计算:多个注意力头可以并行计算,提高效率。
-
位置编码(Positional Encoding)
由于 Transformer 没有显式的序列信息(如 RNN 中的时间步),位置编码被用来为输入序列中的每个词添加位置信息。通常使用正弦和余弦函数生成位置编码:

-
编码器-解码器架构
Transformer 模型由编码器和解码器两部分组成:
- 编码器:将输入序列转换为一系列隐藏表示。每个编码器层包含一个自注意力机制和一个前馈神经网络。
- 解码器:根据编码器的输出生成目标序列。每个解码器层包含两个注意力机制(自注意力和编码器-解码器注意力)和一个前馈神经网络。
-
前馈神经网络(Feed-Forward Neural Network)
每个编码器和解码器层都包含一个前馈神经网络,通常由两个全连接层组成,中间使用 ReLU 激活函数。 -
残差连接和层归一化
为了稳定训练过程,每个子层(如自注意力层和前馈神经网络)后面都会接一个残差连接和层归一化(Layer Normalization)。
Transformer 的优势
-
并行计算:Transformer 可以同时处理整个输入序列,充分利用现代硬件的并行计算能力。
-
长距离依赖:自注意力机制能够捕捉序列中任意两个位置之间的依赖关系,解决了 RNN 的梯度消失问题。
-
可扩展性:Transformer 模型可以通过堆叠更多的层来提升性能,例如 BERT 和 GPT 等模型。
PyTorch 实现 Transformer 的示例:
import torch
import torch.nn as nn
import torch.optim as optimclass TransformerModel(nn.Module):def __init__(self, input_dim, model_dim, num_heads, num_layers, output_dim):super(TransformerModel, self).__init__()self.embedding = nn.Embedding(input_dim, model_dim)self.positional_encoding = nn.Parameter(torch.zeros(1, 1000, model_dim)) # 假设序列长度最大为1000self.transformer = nn.Transformer(d_model=model_dim, nhead=num_heads, num_encoder_layers=num_layers)self.fc = nn.Linear(model_dim, output_dim)def forward(self, src, tgt):src_seq_length, tgt_seq_length = src.size(1), tgt.size(1)src = self.embedding(src) + self.positional_encoding[:, :src_seq_length, :]tgt = self.embedding(tgt) + self.positional_encoding[:, :tgt_seq_length, :]transformer_output = self.transformer(src, tgt)output = self.fc(transformer_output)return output# 超参数
input_dim = 10000 # 词汇表大小
model_dim = 512 # 模型维度
num_heads = 8 # 多头注意力头数
num_layers = 6 # 编码器和解码器层数
output_dim = 10000 # 输出维度(通常与词汇表大小相同)# 初始化模型、损失函数和优化器
model = TransformerModel(input_dim, model_dim, num_heads, num_layers, output_dim)
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)# 假设输入数据
src = torch.randint(0, input_dim, (10, 32)) # (序列长度, 批量大小)
tgt = torch.randint(0, input_dim, (20, 32)) # (序列长度, 批量大小)# 前向传播
output = model(src, tgt)# 计算损失
loss = criterion(output.view(-1, output_dim), tgt.view(-1))# 反向传播和优化
optimizer.zero_grad()
loss.backward()
optimizer.step()print("Loss:", loss.item())
数据处理与加载
在 PyTorch 中,处理和加载数据是深度学习训练过程中的关键步骤。
为了高效地处理数据,PyTorch 提供了强大的工具,包括 torch.utils.data.Dataset 和 torch.utils.data.DataLoader,帮助我们管理数据集、批量加载和数据增强等任务。
PyTorch 数据处理与加载的介绍:
- 自定义 Dataset:通过继承
torch.utils.data.Dataset来加载自己的数据集。 - DataLoader:
DataLoader按批次加载数据,支持多线程加载并进行数据打乱。 - 数据预处理与增强:使用
torchvision.transforms进行常见的图像预处理和增强操作,提高模型的泛化能力。 - 加载标准数据集:
torchvision.datasets提供了许多常见的数据集,简化了数据加载过程。 - 多个数据源:通过组合多个
Dataset实例来处理来自不同来源的数据。
自定义 Dataset
torch.utils.data.Dataset 是一个抽象类,允许你从自己的数据源中创建数据集。
我们需要继承该类并实现以下两个方法:
__len__(self):返回数据集中的样本数量。__getitem__(self, idx):通过索引返回一个样本。
假设我们有一个简单的 CSV 文件或一些列表数据,我们可以通过继承 Dataset 类来创建自己的数据集。
import torch
from torch.utils.data import Dataset# 自定义数据集类
class MyDataset(Dataset):def __init__(self, X_data, Y_data):"""初始化数据集,X_data 和 Y_data 是两个列表或数组X_data: 输入特征Y_data: 目标标签"""self.X_data = X_dataself.Y_data = Y_datadef __len__(self):"""返回数据集的大小"""return len(self.X_data)def __getitem__(self, idx):"""返回指定索引的数据"""x = torch.tensor(self.X_data[idx], dtype=torch.float32) # 转换为 Tensory = torch.tensor(self.Y_data[idx], dtype=torch.float32)return x, y# 示例数据
X_data = [[1, 2], [3, 4], [5, 6], [7, 8]] # 输入特征
Y_data = [1, 0, 1, 0] # 目标标签# 创建数据集实例
dataset = MyDataset(X_data, Y_data)
print(dataset.X_data) # [[1, 2], [3, 4], [5, 6], [7, 8]]
print(dataset.Y_data) # [1, 0, 1, 0]
使用 DataLoader 加载数据
DataLoader 是 PyTorch 提供的一个重要工具,用于从 Dataset 中按批次(batch)加载数据。
DataLoader 允许我们批量读取数据并进行多线程加载,从而提高训练效率。
# 创建数据集实例 (自定义 Dataset)
dataset = MyDataset(X_data, Y_data)from torch.utils.data import DataLoader# 创建 DataLoader 实例
# batch_size 设置每次加载的样本数量
# shuffle: 是否对数据进行洗牌,通常训练时需要将数据打乱。
dataloader = DataLoader(dataset, batch_size=2, shuffle=True)# 打印加载的数据
for epoch in range(1):for batch_idx, (inputs, labels) in enumerate(dataloader):print(f'Batch {batch_idx + 1}:')print(f'Inputs: {inputs}')print(f'Labels: {labels}')# Batch 1:
# Inputs: tensor([[7., 8.],
# [1., 2.]])
# Labels: tensor([0., 1.])
# Batch 2:
# Inputs: tensor([[3., 4.],
# [5., 6.]])
每次循环中,DataLoader 会返回一个批次的数据,包括输入特征(inputs)和目标标签(labels)。
预处理与数据增强
数据预处理和增强对于提高模型的性能至关重要。
PyTorch 提供了 torchvision.transforms 模块来进行常见的图像预处理和增强操作,如旋转、裁剪、归一化等。
常见的图像预处理操作:
import torchvision.transforms as transforms
from PIL import Image# 定义数据预处理的流水线, transforms.Compose():将多个变换操作组合在一起。
transform = transforms.Compose([transforms.Resize((128, 128)), # 将图像调整为 128x128transforms.ToTensor(), # 将图像转换为张量,值会被归一化到 [0, 1] 范围transforms.Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225]) # 标准化
])# 加载图像
image = Image.open('image.jpg')# 应用预处理
image_tensor = transform(image)
print(image_tensor.shape) # 输出张量的形状
图像数据增强
数据增强技术通过对训练数据进行随机变换,增加数据的多样性,帮助模型更好地泛化。例如,随机翻转、旋转、裁剪等。
transform = transforms.Compose([transforms.RandomHorizontalFlip(), # 随机水平翻转transforms.RandomRotation(30), # 随机旋转 30 度transforms.RandomResizedCrop(128), # 随机裁剪并调整为 128x128transforms.ToTensor(),transforms.Normalize(mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225])
])
加载图像数据集
对于图像数据集,torchvision.datasets 提供了许多常见数据集(如 CIFAR-10、ImageNet、MNIST 等)以及用于加载图像数据的工具。
加载 MNIST 数据集:
import torchvision.datasets as datasets
import torchvision.transforms as transforms# 定义预处理操作
transform = transforms.Compose([transforms.ToTensor(),transforms.Normalize((0.5,), (0.5,)) # 对灰度图像进行标准化
])# 下载并加载 MNIST 数据集, train=True 和 train=False 分别表示训练集和测试集。
train_dataset = datasets.MNIST(root='./data', train=True, download=True, transform=transform)
test_dataset = datasets.MNIST(root='./data', train=False, download=True, transform=transform)# 创建 DataLoader
train_loader = DataLoader(train_dataset, batch_size=64, shuffle=True)
test_loader = DataLoader(test_dataset, batch_size=64, shuffle=False)# 迭代训练数据
for inputs, labels in train_loader:print(inputs.shape) # 每个批次的输入数据形状print(labels.shape) # 每个批次的标签形状
用多个数据源(Multi-source Dataset)
如果你的数据集由多个文件、多个来源(例如多个图像文件夹)组成,可以通过继承 Dataset 类自定义加载多个数据源。
PyTorch 提供了 ConcatDataset 和 ChainDataset 等类来连接多个数据集。
例如,假设我们有多个图像文件夹的数据,可以将它们合并为一个数据集:
from torch.utils.data import ConcatDataset# 假设 dataset1 和 dataset2 是两个 Dataset 对象
combined_dataset = ConcatDataset([dataset1, dataset2])
combined_loader = DataLoader(combined_dataset, batch_size=64, shuffle=True)
实现二分类模型
本章节将使用 PyTorch 实现一个简单的 前馈神经网络(Feedforward Neural Network),用于解决 二分类任务。
- 网络结构设计
• 输入层:接收特征数据
• 隐藏层:全连接层(Linear Layer) + ReLU 激活函数
• 输出层:单神经元输出 + Sigmoid 激活函数(将结果映射到 [0, 1] 区间)
-
训练配置
组件 选择 作用 损失函数 nn.MSELoss()计算预测值与真实标签的均方误差 优化器 optim.SGD()随机梯度下降优化器,用于参数更新
- 训练流程
- 前向传播
• 数据通过隐藏层和输出层,生成预测值。 - 损失计算
• 使用均方误差(MSE)衡量预测与目标的差异。 - 反向传播
• 自动计算各参数的梯度(loss.backward())。 - 参数更新
• 优化器根据梯度调整权重(optimizer.step())。
- 前向传播
示例
# 导入PyTorch库
import torch
import torch.nn as nn# 定义输入层大小、隐藏层大小、输出层大小和批量大小
n_in, n_h, n_out = 10, 5, 1
batch_size = 10# 创建虚拟输入数据和目标数据
x = torch.randn(batch_size, n_in) # 随机生成输入数据
y = torch.tensor([[1.0], [0.0], [0.0], [1.0], [1.0], [1.0], [0.0], [0.0], [1.0], [1.0]]) # 目标输出数据# 创建顺序模型,包含线性层、ReLU激活函数和Sigmoid激活函数
model = nn.Sequential(nn.Linear(n_in, n_h), # 输入层到隐藏层的线性变换(输入特征是 10 个,隐藏层有 5 个神经元)nn.ReLU(), # 隐藏层的ReLU激活函数(引入非线性变换,增强模型的表达能力)nn.Linear(n_h, n_out), # 隐藏层到输出层的线性变换(输出为 1 个神经元)nn.Sigmoid() # 输出层的Sigmoid激活函数(将输出压缩到[0,1]区间)
)# ReLU: 隐藏层使用 → 特征非线性化
# ↑ ↓
# Sigmoid: 输出层使用 → 结果概率化# 定义均方误差损失函数和随机梯度下降优化器
criterion = torch.nn.MSELoss() # 使用均方误差损失函数
optimizer = torch.optim.SGD(model.parameters(), lr=0.01) # 学习率为0.01# 执行梯度下降算法进行模型训练
for epoch in range(50): # 迭代50次y_pred = model(x) # 前向传播,计算预测值loss = criterion(y_pred, y) # 计算损失print('epoch: ', epoch, 'loss: ', loss.item()) # 打印损失值optimizer.zero_grad() # 清零梯度loss.backward() # 反向传播,计算当前batch梯度optimizer.step() # 用当前梯度更新参数
epoch: 0 loss: 0.27662041783332825
epoch: 1 loss: 0.2763134837150574
epoch: 2 loss: 0.2760070562362671
…
epoch: 25 loss: 0.26908987760543823
epoch: 26 loss: 0.2687944769859314
epoch: 27 loss: 0.2684994637966156
…
epoch: 47 loss: 0.2629861533641815
epoch: 48 loss: 0.26272860169410706
epoch: 49 loss: 0.2624712884426117
为什么每次循环都要清零梯度?
在PyTorch训练过程中每次循环都要调用 optimizer.zero_grad() 清零梯度,主要有以下三个关键原因:
-
梯度累积问题(核心原因)
- PyTorch默认会累积梯度(即每次
loss.backward()时梯度会累加到原有梯度上) - 不清零会导致梯度值越来越大,参数更新失控
- 示例说明:
# 不清零时梯度变化: 第一次迭代:grad = 0.1 第二次迭代:grad = 0.1 + 0.1 = 0.2 第三次迭代:grad = 0.2 + 0.1 = 0.3
- PyTorch默认会累积梯度(即每次
-
训练稳定性要求
- 每个 batch 的数据特征不同,需要独立计算梯度
- 保持每次参数更新只基于当前 batch 的梯度信息
- 避免历史梯度干扰当前参数更新方向
可视化
# 用于存储每轮的损失值
losses = []# 执行梯度下降算法进行模型训练
for epoch in range(50): # 迭代50次y_pred = model(x) # 前向传播,计算预测值loss = criterion(y_pred, y) # 计算损失losses.append(loss.item()) # 记录损失值print(f'Epoch [{epoch+1}/50], Loss: {loss.item():.4f}') # 打印损失值optimizer.zero_grad() # 清零梯度loss.backward() # 反向传播,计算梯度optimizer.step() # 更新模型参数# 可视化损失变化曲线
plt.figure(figsize=(8, 5))
plt.plot(range(1, 51), losses, label='Loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.title('Training Loss Over Epochs')
plt.legend()
plt.grid()
plt.show()# 可视化预测结果与实际目标值对比
y_pred_final = model(x).detach().numpy() # 最终预测值
y_actual = y.numpy() # 实际值plt.figure(figsize=(8, 5))
plt.plot(range(1, batch_size + 1), y_actual, 'o-', label='Actual', color='blue')
plt.plot(range(1, batch_size + 1), y_pred_final, 'x--', label='Predicted', color='red')
plt.xlabel('Sample Index')
plt.ylabel('Value')
plt.title('Actual vs Predicted Values')
plt.legend()
plt.grid()
plt.show()
显示如下所示:

实现线性回归模型
线性回归通过拟合一个线性函数来预测输出。
对于一个简单的线性回归问题,模型可以表示为:

可视化:

在 PyTorch 中,线性回归模型可以通过继承 nn.Module 类来实现。我们将通过一个简单的示例来详细说明如何使用 PyTorch 实现线性回归模型。
数据准备
我们首先准备一些假数据,用于训练我们的线性回归模型。这里,我们可以生成一个简单的线性关系的数据集,其中每个样本有两个特征 x1,x2。
import torch
import matplotlib.pyplot as plt# 随机种子,确保每次运行结果一致
torch.manual_seed(42)# 生成训练数据
X = torch.randn(100, 2) # 生成100个样本,每个样本有2个特征,数据服从标准正态分布
true_w = torch.tensor([2.0, 3.0]) # 假设真实权重
true_b = 4.0 # 偏置项
Y = X @ true_w + true_b + torch.randn(100) * 0.1 # 计算目标值 Y = X * w + b + 噪声,其中噪声是标准差为 0.1 的正态分布# 打印部分数据
print(X[:5])
# tensor([[ 1.9269, 1.4873],
# [ 0.9007, -2.1055],
# [ 0.6784, -1.2345],
# [-0.0431, -1.6047],
# [-0.7521, 1.6487]])print(Y[:5])
# tensor([12.4460, -0.4663, 1.7666, -0.9357, 7.4781])
这段代码创建了一个带有噪声的线性数据集,输入 X 为 100 x 2 的矩阵,每个样本有两个特征,输出 Y 由真实的权重和偏置生成,并加上了一些随机噪声。
定义线性回归模型
可以通过继承 nn.Module 来定义一个简单的线性回归模型。在 PyTorch 中,线性回归的核心是 nn.Linear() 层,它会自动处理权重和偏置的初始化。
import torch.nn as nn# 定义线性回归模型
class LinearRegressionModel(nn.Module):def __init__(self):super(LinearRegressionModel, self).__init__()# 定义一个线性层,输入为2个特征,输出为1个预测值self.linear = nn.Linear(2, 1) # 输入维度2,输出维度1def forward(self, x):return self.linear(x) # 前向传播,返回预测结果# 创建模型实例
model = LinearRegressionModel()
这里的 nn.Linear(2, 1) 表示一个线性层,它有 2 个输入特征和 1 个输出。forward 方法定义了如何通过这个层进行前向传播。
定义损失函数与优化器
线性回归的常见损失函数是 均方误差损失(MSELoss),用于衡量预测值与真实值之间的差异。PyTorch 中提供了现成的 MSELoss 函数。
我们将使用 SGD(随机梯度下降) 或 Adam 优化器来最小化损失函数。
# 损失函数(均方误差), 计算预测值与真实值的均方误差
criterion = nn.MSELoss()# 优化器(使用 SGD 或 Adam)
optimizer = torch.optim.SGD(model.parameters(), lr=0.01) # 学习率设置为0.01
训练模型
在训练过程中,我们将执行以下步骤:
- 使用输入数据 X 进行前向传播,得到预测值。
- 计算损失(预测值与实际值之间的差异)。
- 使用反向传播计算梯度。
- 更新模型参数(权重和偏置)。
我们将训练模型 1000 轮,并在每 100 轮打印一次损失。
# 训练模型
num_epochs = 1000 # 训练 1000 轮
for epoch in range(num_epochs):model.train() # 设置模型为训练模式# 前向传播predictions = model(X) # 模型输出预测值loss = criterion(predictions.squeeze(), Y) # 计算损失(注意预测值需要压缩为1D)# predictions.squeeze():我们在这里将模型的输出从 2D 张量压缩为 1D,因为目标值 Y 是一个一维数组。# 反向传播optimizer.zero_grad() # 每次反向传播前需要清空之前的梯度。loss.backward() # 计算梯度optimizer.step() # 更新权重和偏置参数# 打印损失if (epoch + 1) % 100 == 0:print(f'Epoch [{epoch + 1}/1000], Loss: {loss.item():.4f}')# Epoch[100 / 1000], Loss: 0.4569
# Epoch[200 / 1000], Loss: 0.0142
# ...
# Epoch[900 / 1000], Loss: 0.0081
# Epoch[1000 / 1000], Loss: 0.0081
评估模型
训练完成后,我们可以通过查看模型的权重和偏置来评估模型的效果。我们还可以在新的数据上进行预测并与实际值进行比较。
# 查看训练后的权重和偏置
print(f'Predicted weight: {model.linear.weight.data.numpy()}')
# Predicted weight: [[2.009702 2.9986038]]
print(f'Predicted bias: {model.linear.bias.data.numpy()}')
# Predicted bias: [4.020908]# 在新数据上做预测
with torch.no_grad(): # 评估时不需要计算梯度predictions = model(X)# 可视化预测与实际值
plt.scatter(X[:, 0], Y, color='blue', label='True values')
plt.scatter(X[:, 0], predictions, color='red', label='Predictions')
plt.legend()
plt.show()
查看训练后的权重和偏置,分别为 [2.009702 2.9986038], [4.020908], 非常接近预定的 [2,3], [4]
结果分析
在训练过程中,随着损失逐渐减小,我们希望最终的模型能够拟合我们生成的数据。通过查看训练后的权重和偏置,我们可以比较其与真实值(true_w 和 true_b)的差异。理论上,模型的输出权重应该接近 true_w 和 true_b。

在可视化的散点图中,蓝色点表示真实值,红色点表示模型的预测值。我们希望看到红色点与蓝色点尽可能接近,表明模型成功学习了数据的线性关系。
手写数字识别(使用CNN)
以下示例展示如何用 PyTorch 构建一个简单的 CNN 模型,用于 MNIST 数据集的数字分类。
主要步骤:
- 数据加载与预处理:使用 torchvision 加载和预处理 MNIST 数据。
- 模型构建:定义卷积层、池化层和全连接层。
- 训练:通过损失函数和优化器进行模型训练。
- 评估:测试集上计算模型的准确率。
- 可视化:展示部分测试样本及其预测结果。
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
import matplotlib.pyplot as plt# 临时解决 SSL 证书问题
import ssl
ssl._create_default_https_context = ssl._create_unverified_context# 1. 数据加载与预处理
transform = transforms.Compose([transforms.ToTensor(), # 将PIL图像转为张量transforms.Normalize((0.5,), (0.5,)) # 归一化到[-1,1]范围
])# 加载 MNIST 数据集
train_dataset = datasets.MNIST(root='./data', train=True, transform=transform, download=True)
test_dataset = datasets.MNIST(root='./data', train=False, transform=transform, download=True)# 创建数据加载器
train_loader = torch.utils.data.DataLoader(dataset=train_dataset, batch_size=64, shuffle=True)
test_loader = torch.utils.data.DataLoader(dataset=test_dataset, batch_size=64, shuffle=False)# 2. 定义 CNN 模型
class SimpleCNN(nn.Module):def __init__(self):super(SimpleCNN, self).__init__()# 定义卷积层self.conv1 = nn.Conv2d(1, 32, kernel_size=3, stride=1, padding=1) # 输入1通道,输出32通道self.conv2 = nn.Conv2d(32, 64, kernel_size=3, stride=1, padding=1) # 输入32通道,输出64通道# 定义全连接层self.fc1 = nn.Linear(64 * 7 * 7, 128) # 展平后输入到全连接层self.fc2 = nn.Linear(128, 10) # 10 个类别def forward(self, x):x = F.relu(self.conv1(x)) # 第一层卷积 + ReLUx = F.max_pool2d(x, 2) # 最大池化,[batch_size, 32, 14, 14]x = F.relu(self.conv2(x)) # 第二层卷积 + ReLUx = F.max_pool2d(x, 2) # 最大池化,[batch_size, 64, 7, 7]x = x.view(-1, 64 * 7 * 7) # 展平x = F.relu(self.fc1(x)) # 全连接层 + ReLUx = self.fc2(x) # 最后一层输出return x# 创建模型实例
model = SimpleCNN()# 3. 定义损失函数与优化器
criterion = nn.CrossEntropyLoss() # 多分类交叉熵损失
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.9) # 学习率和动量# 4. 模型训练
num_epochs = 5
model.train() # 设置模型为训练模式for epoch in range(num_epochs):total_loss = 0for images, labels in train_loader:outputs = model(images) # 前向传播loss = criterion(outputs, labels) # 计算损失optimizer.zero_grad() # 清空梯度loss.backward() # 反向传播optimizer.step() # 更新参数total_loss += loss.item()print(f"Epoch [{epoch + 1}/{num_epochs}], Loss: {total_loss / len(train_loader):.4f}")# Epoch [1/5], Loss: 0.2370
# Epoch [2/5], Loss: 0.0539
# Epoch [3/5], Loss: 0.0383
# Epoch [4/5], Loss: 0.0292
# Epoch [5/5], Loss: 0.0221# 5. 模型测试
model.eval() # 设置模型为评估模式
correct = 0
total = 0with torch.no_grad(): # 关闭梯度计算,以提高效率for images, labels in test_loader: # 在测试集上评估模型准确率outputs = model(images)_, predicted = torch.max(outputs, 1)total += labels.size(0)correct += (predicted == labels).sum().item()accuracy = 100 * correct / total
print(f"Test Accuracy: {accuracy:.2f}%")
# Test Accuracy: 98.87%# 6. 可视化测试结果
dataiter = iter(test_loader)
images, labels = next(dataiter)
outputs = model(images)
_, predictions = torch.max(outputs, 1)fig, axes = plt.subplots(1, 6, figsize=(12, 4))
for i in range(6): # 随机选取6个测试样本, 显示图像、真实标签和预测结果axes[i].imshow(images[i][0], cmap='gray')axes[i].set_title(f"Label: {labels[i]}\nPred: {predictions[i]}")axes[i].axis('off')
plt.show()

序列数据并进行分类(RNN)
import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt
import numpy as np# 数据集:字符序列预测(Hello -> Elloh)
char_set = list("hello")
char_to_idx = {c: i for i, c in enumerate(char_set)}
idx_to_char = {i: c for i, c in enumerate(char_set)}# 数据准备
input_str = "hello"
target_str = "elloh"
input_data = [char_to_idx[c] for c in input_str]
target_data = [char_to_idx[c] for c in target_str]# 转换为独热编码
input_one_hot = np.eye(len(char_set))[input_data]
print("input_one_hot : ", input_one_hot)
# input_one_hot : [[1. 0. 0. 0. 0.]
# [0. 1. 0. 0. 0.]
# [0. 0. 0. 1. 0.]
# [0. 0. 0. 1. 0.]
# [0. 0. 0. 0. 1.]]# 转换为 PyTorch Tensor
inputs = torch.tensor(input_one_hot, dtype=torch.float32)
targets = torch.tensor(target_data, dtype=torch.long)# 模型超参数
input_size = len(char_set)
hidden_size = 8
output_size = len(char_set)
num_epochs = 200
learning_rate = 0.1# 定义 RNN 模型
class RNNModel(nn.Module):def __init__(self, input_size, hidden_size, output_size):super(RNNModel, self).__init__()self.rnn = nn.RNN(input_size, hidden_size, batch_first=True) # 定义 RNN 层self.fc = nn.Linear(hidden_size, output_size) # 加入全连接层 torch.nn.Linear 用于映射隐藏状态到输出。def forward(self, x, hidden):out, hidden = self.rnn(x, hidden)out = self.fc(out) # 应用全连接层return out, hiddenmodel = RNNModel(input_size, hidden_size, output_size)# 定义损失函数和优化器
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=learning_rate)# 训练 RNN
losses = []
hidden = None # 初始隐藏状态为 None
for epoch in range(num_epochs):optimizer.zero_grad()# 前向传播outputs, hidden = model(inputs.unsqueeze(0), hidden)hidden = hidden.detach() # 隐藏状态通过 hidden.detach() 防止梯度爆炸。# 计算损失loss = criterion(outputs.view(-1, output_size), targets)loss.backward()optimizer.step()losses.append(loss.item())if (epoch + 1) % 20 == 0:print(f"Epoch [{epoch + 1}/{num_epochs}], Loss: {loss.item():.4f}")# Epoch [20/200], Loss: 0.0019
# Epoch [40/200], Loss: 0.0003
# Epoch [60/200], Loss: 0.0002
# Epoch [80/200], Loss: 0.0002
# Epoch [100/200], Loss: 0.0001
# Epoch [120/200], Loss: 0.0001
# Epoch [140/200], Loss: 0.0001
# Epoch [160/200], Loss: 0.0001
# Epoch [180/200], Loss: 0.0001
# Epoch [200/200], Loss: 0.0001# 测试 RNN
with torch.no_grad():test_hidden = Nonetest_output, _ = model(inputs.unsqueeze(0), test_hidden)predicted = torch.argmax(test_output, dim=2).squeeze().numpy()print("Input sequence: ", ''.join([idx_to_char[i] for i in input_data]))# Input sequence: helloprint("Predicted sequence: ", ''.join([idx_to_char[i] for i in predicted]))# Predicted sequence: elloh# 可视化损失
plt.plot(losses, label="Training Loss")
plt.xlabel("Epoch")
plt.ylabel("Loss")
plt.title("RNN Training Loss Over Epochs")
plt.legend()
plt.show()

