一般个人网址是什么_吉林省吉林市为什么名字一样_搜索大全引擎地址_网络营销教程

Description

You are given an integer n and a 2D integer array queries.

There are n cities numbered from 0 to n - 1. Initially, there is a unidirectional road from city i to city i + 1 for all 0 <= i < n - 1.

queries[i] = [ui, vi] represents the addition of a new unidirectional road from city ui to city vi. After each query, you need to find the length of the shortest path from city 0 to city n - 1.

Return an array answer where for each i in the range [0, queries.length - 1], answer[i] is the length of the shortest path from city 0 to city n - 1 after processing the first i + 1 queries.

Example 1:

Input: n = 5, queries = [[2,4],[0,2],[0,4]]Output: [3,2,1]Explanation:

After the addition of the road from 2 to 4, the length of the shortest path from 0 to 4 is 3.

After the addition of the road from 0 to 2, the length of the shortest path from 0 to 4 is 2.

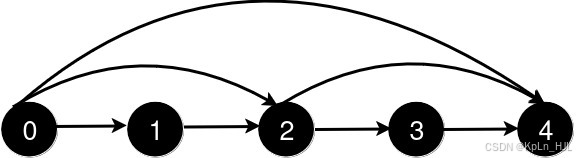
After the addition of the road from 0 to 4, the length of the shortest path from 0 to 4 is 1.

Example 2:

Input: n = 4, queries = [[0,3],[0,2]]Output: [1,1]Explanation:

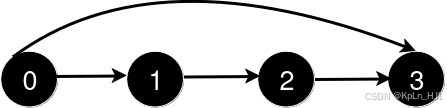
After the addition of the road from 0 to 3, the length of the shortest path from 0 to 3 is 1.

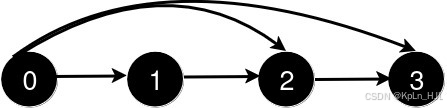
After the addition of the road from 0 to 2, the length of the shortest path remains 1.

Constraints:

3 <= n <= 500
1 <= queries.length <= 500
queries[i].length == 2
0 <= queries[i][0] < queries[i][1] < n
1 < queries[i][1] - queries[i][0]
There are no repeated roads among the queries.

Solution

Intuitive

Use a list to store the original path, and a hash map to store the node’s neighbors. When there’s a new path/query, change the node distance and all the distances after that node.

Time complexity: $o(n\ast n)$
Space complexity: $o(n)$

Code

Intuitive

class Solution:def shortestDistanceAfterQueries(self, n: int, queries: List[List[int]]) -> List[int]:distance = list(range(n))neighbor = {i + 1: [i] for i in range(n)}res = []for each_query in queries:each_query.sort()start_city, end_city = each_queryneighbor[end_city].append(start_city)distance[end_city] = min(distance[neighbor_city] + 1 for neighbor_city in neighbor[end_city])# update all the cities at the rightprev_city = end_cityfor right_city in range(end_city + 1, n):distance[right_city] = min(distance[neighbor_city] + 1 for neighbor_city in neighbor[right_city])prev_city += 1res.append(distance[-1])return res