目录
1 初识Numpy
1.1 Numpy介绍
1.2 ndarray介绍
1.3 ndarray与Python原生list运算效率对比
1.4 ndarray的优势
2 N维数组--ndarray
2.1 ndarray的属性
2.2 ndarray的形状
2.3 ndarray的类型
3 基本操作--生成数组的方法
3.1 生成0和1的数组
3.2 从现有数组生成
3.3 生成固定范围
3.4 生成随机数组
4 基本操作--数组的索引、切片
5 基本操作--形状修改
5.1 reshape
5.2 resize
5.3 T(转置)
6 基本操作--类型修改
6.1 astype
6.2 tostring
7 基本操作--数组的去重
7.1 unique
8 ndarray运算
8.1 逻辑运算
8.2 通用判断函数
8.3 np.where(三元运算符)
8.4 统计运算
9 数组间运算
9.1 数组与数的运算
9.2 数组与数组的运算
10 矩阵乘法运算
10.1 矩阵和标量的乘法
10.2 矩阵和矩阵/向量的乘法
1 初识Numpy
1.1 Numpy介绍
Numpy是一个开源的Python科学计算库,用于快速处理多维数组。
Numpy支持常见的数组和矩阵操作。对于同样的数值计算任务,使用Numpy比直接使用Python简洁的多。
Numpy使用ndarray对象来处理多维数组,该对象是一个快速而灵活的大数据容器。
1.2 ndarray介绍
Numpy提供了一个N维数组类型ndarray,它描述了相同类型的“items”的集合。
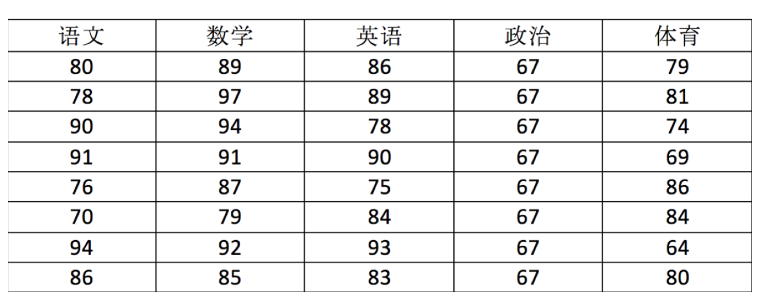
用ndarray进行存储:
import numpy as np# 创建ndarray
score = np.array(
[[80, 89, 86, 67, 79],
[78, 97, 89, 67, 81],
[90, 94, 78, 67, 74],
[91, 91, 90, 67, 69],
[76, 87, 75, 67, 86],
[70, 79, 84, 67, 84],
[94, 92, 93, 67, 64],
[86, 85, 83, 67, 80]])score
1.3 ndarray与Python原生list运算效率对比
import random
import time
import numpy as np
a = []
for i in range(100000000):a.append(random.random())# 通过%time魔法方法, 查看当前行的代码运行一次所花费的时间
%time sum1=sum(a)b=np.array(a)%time sum2=np.sum(b)
其中第一个内容是使用原生Python计算时间,第二个内容是使用Numpy计算时间。
可以看到,使用Numpy计算时间少些,适用于机器学习中大量的数据运算。
1.4 ndarray的优势
1、内存块风格
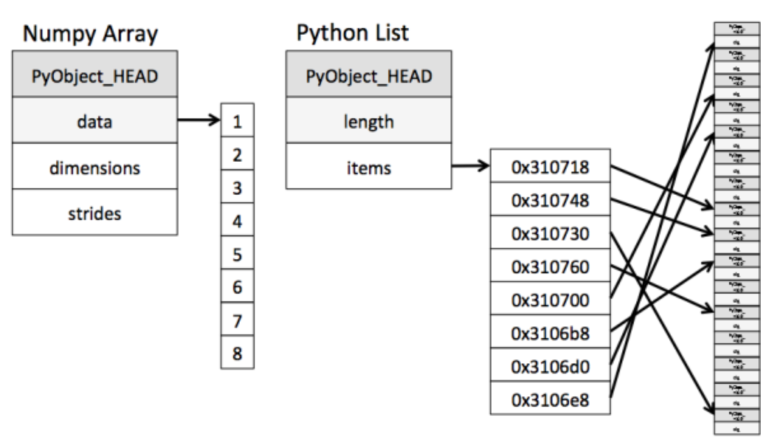
ndarray在存储数据的时候,数据与数据地址是连续的,使得批量处理数据元素速度更快。而python原生list就只能通过寻址方式找到下一个元素。
ndarray中的元素类型都是相同的,而python列表中的元素类型是任意的。
2、ndarray支持并行化运算(向量化运算)
3、ndarray底层是用C语言写的,效率更高,释放了GIL(全局解释锁)
2 N维数组--ndarray
2.1 ndarray的属性
数组属性反映了数组本身固有的信息。
| 属性名字 | 属性解释 |
|---|---|
| ndarray.shape | 数组维度的元组 |
| ndarray.ndim | 数组维数 |
| ndarray.size | 数组中的元素数量 |
| ndarray.itemsize | 一个数组元素的长度(字节) |
| ndarray.dtype | 数组元素的类型 |
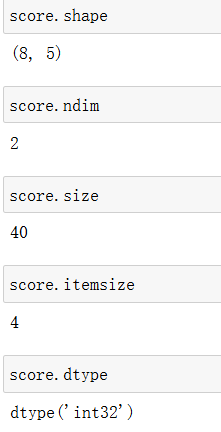
2.2 ndarray的形状
一维数组
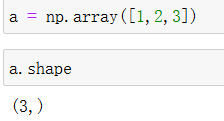
这个一维数组中有3个元素。
二维数组

这个二维数组中有2个一维数组,每个一维数组中有3个元素。
三维数组
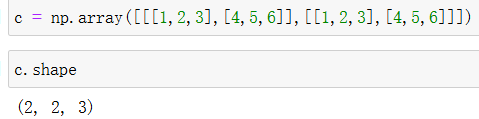
这个三维数组中有2个二维数组,每个二维数组中有2个一维数组,而每个一维数组中有3个元素。
2.3 ndarray的类型
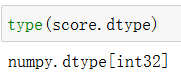
创建数组的时候指定类型
1、单精度浮点数

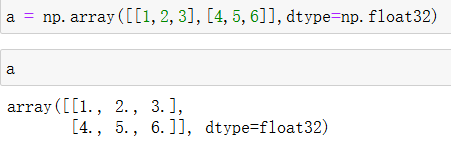
2、字符串
![]()

注:S7表示列表中元素字符个数最大的为7。
3 基本操作--生成数组的方法
3.1 生成0和1的数组

3.2 从现有数组生成
生成方式
np.array(object,dtype) 从现有的数组中创建
np.asarray(object,dtype) 相当于索引形式,并没有真正创建一个新的
关于array和asarray的不同


将a[0,0]修改后,a1[0,0]没有变,而a2[0,0]变了。这是因为a1与a2的生成方式不同。
3.3 生成固定范围
np.linspace (start, stop, num, endpoint)--创建等差数组(指定数量)


np.arange(start,stop,step,dtype)--创建等差数组(指定步长)
step:步长,默认值为1

np.logspace(start,stop,num)--创建等比数列
num:要生成的等比数列数量,默认为50

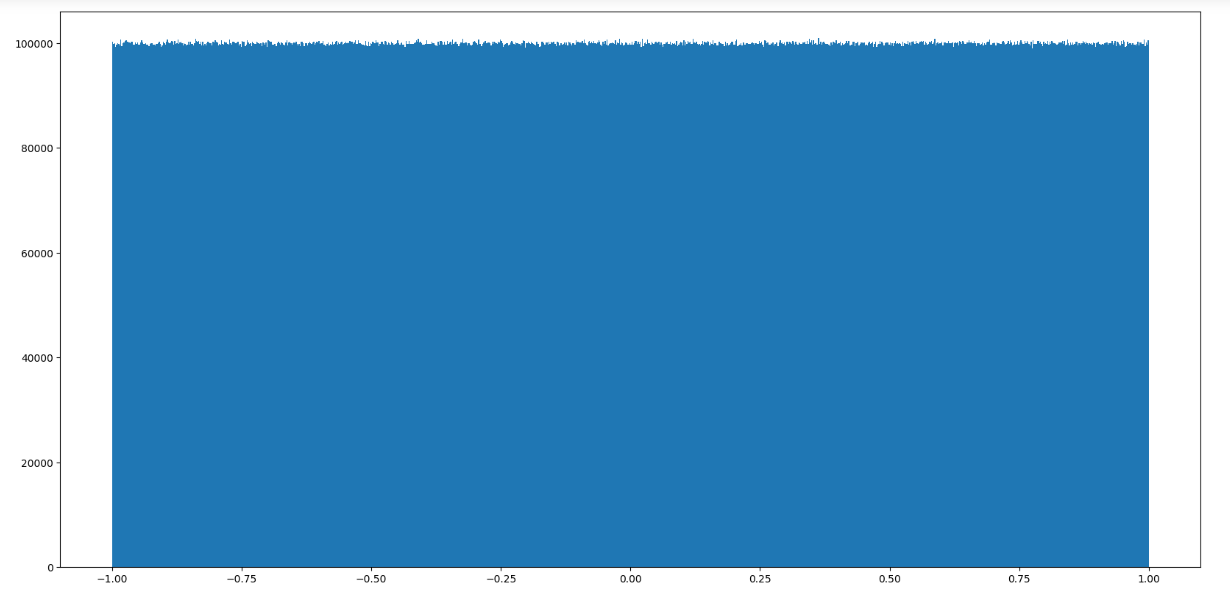
3.4 生成随机数组
正态分布
正态分布是具有两个参数μ和σ的连续型随机变量的分布,第一参数μ是服从正态分布的随机变量的均值,第二个参数σ是此随机变量的标准差,所以正态分布记作N(μ,σ )。
μ决定了其位置,其标准差σ决定了分布的幅度。当μ = 0,σ = 1时的正态分布是标准正态分布。
方差是在概率论和统计方差衡量一组数据时离散程度的度量。
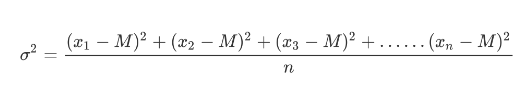
M为平均值,n为数据总个数,σ 为标准差。标准差σ计算如下:
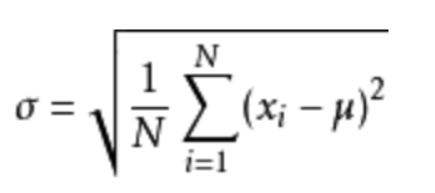
标准差与方差可以理解为数据的一个离散程度的衡量。

np.random.normal(loc=0.0,scale=1.0,size=None)--正态分布创建方式

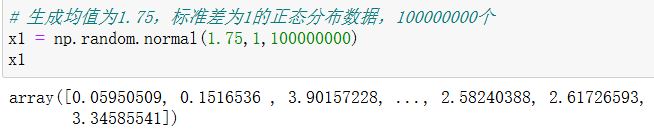

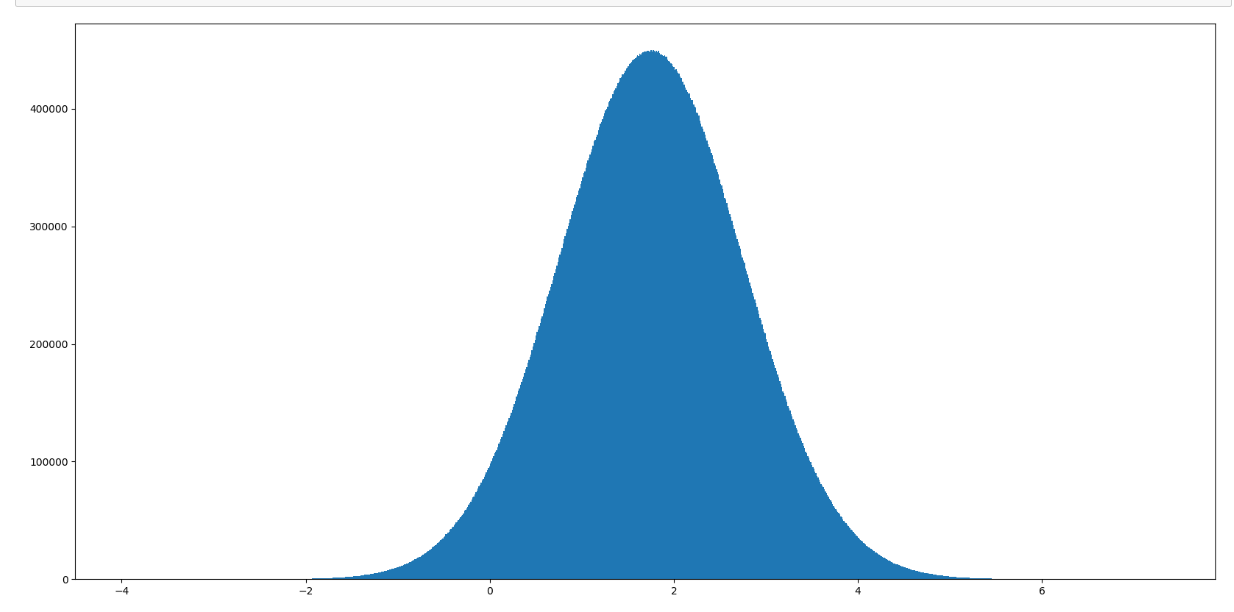

均匀分布
np.random.uniform(low=0.0, high=1.0, size=None)

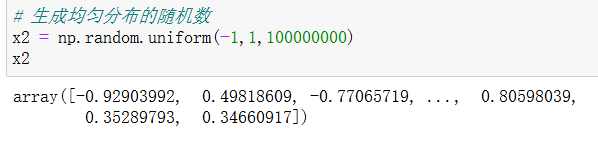

4 基本操作--数组的索引、切片
以二维数组为例:
索引:对象[one][two] 或者 对象[one,two]
切片:对象[one,start:stop]
1、案例:二维数组的切片

2、案例:三维数组的索引
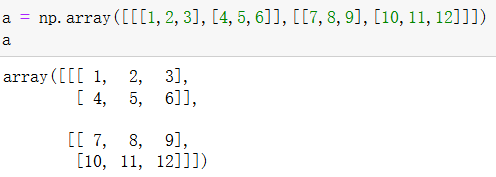
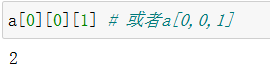
5 基本操作--形状修改
5.1 reshape

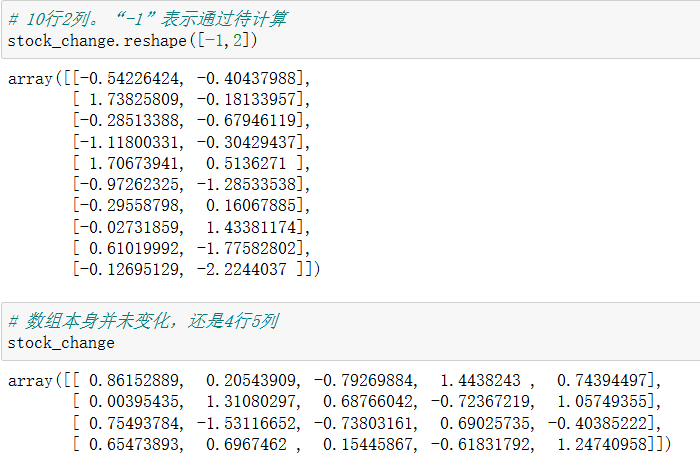
5.2 resize
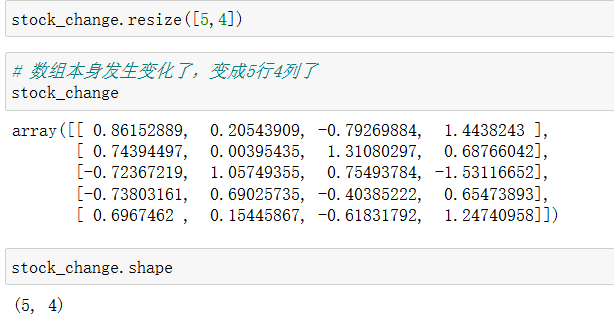
5.3 T(转置)
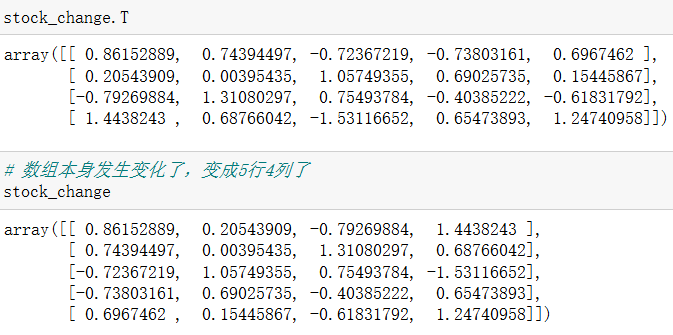
reshape、T使用后即可返回结果,但是数组本身不会发生变化;resize使用后不会返回结果(需要单独输入stock_change这个变量名才能显示结果),但是数组本身发生变化。
6 基本操作--类型修改
6.1 astype

6.2 tostring

7 基本操作--数组的去重
7.1 unique

8 ndarray运算
8.1 逻辑运算

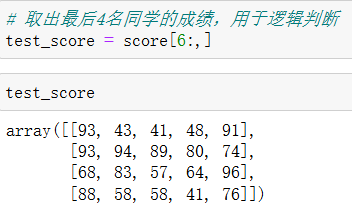
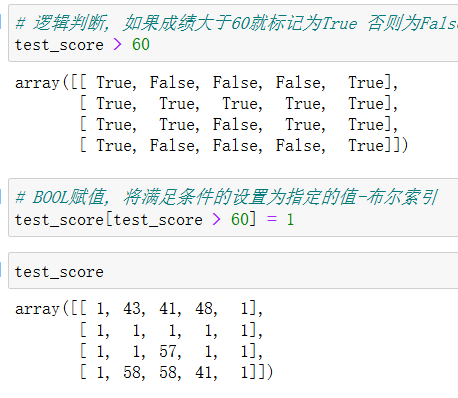
8.2 通用判断函数
np.all()
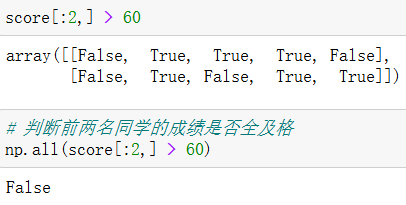
np.any()
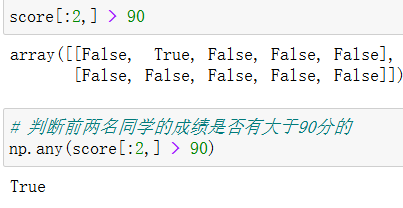
8.3 np.where(三元运算符)
np.where
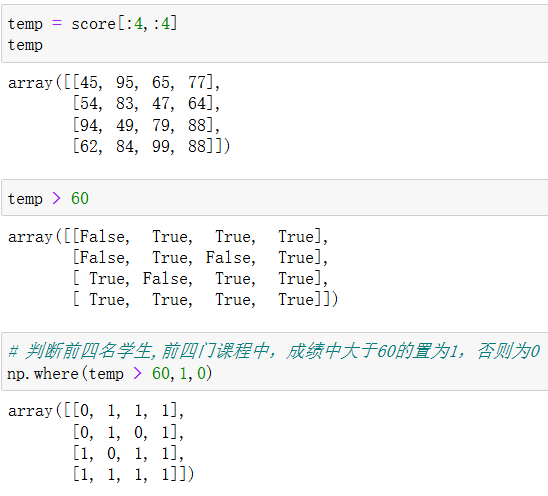
复合逻辑需要结合np.logical_and和np.logical_or使用
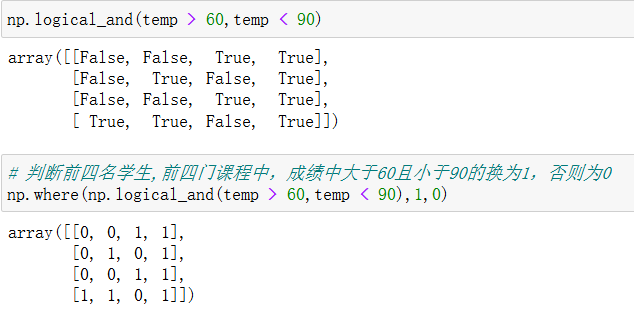
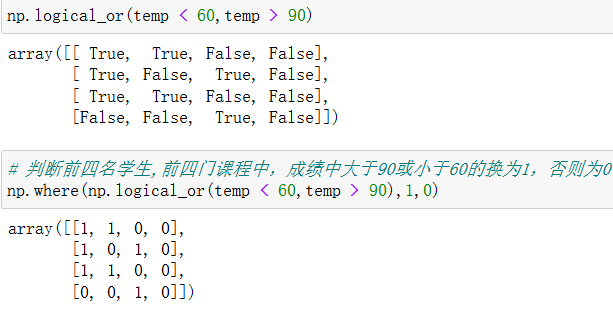
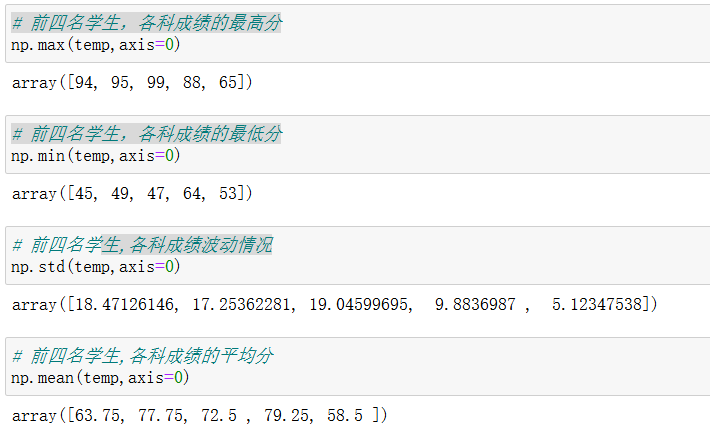
8.4 统计运算
学生成绩统计运算


9 数组间运算
9.1 数组与数的运算


9.2 数组与数组的运算
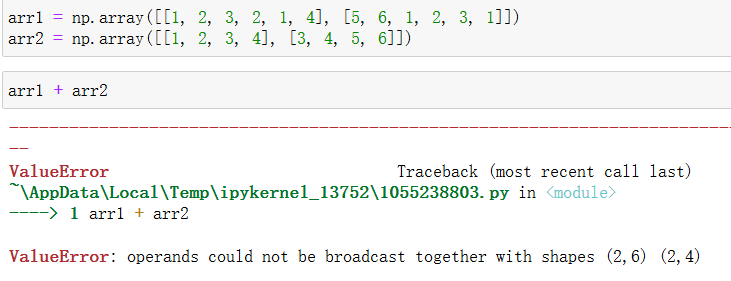
满足广播机制实现的条件(1),但是不满足(2)。所以不能进行arr1+arr2的运算。
广播机制
数组在进行矢量化运算时,要求数组的形状是相等的。当形状不相等的数组执行算术运算的时候,就会出现广播机制,该机制会对数组进行扩展,使数组的shape属性值一样,这样,就可以进行矢量化运算了。
广播机制的实现需要满足下面两个条件:
(1)两个数组的某一维度相等。
(2)其中一个数组的某一维度为1。
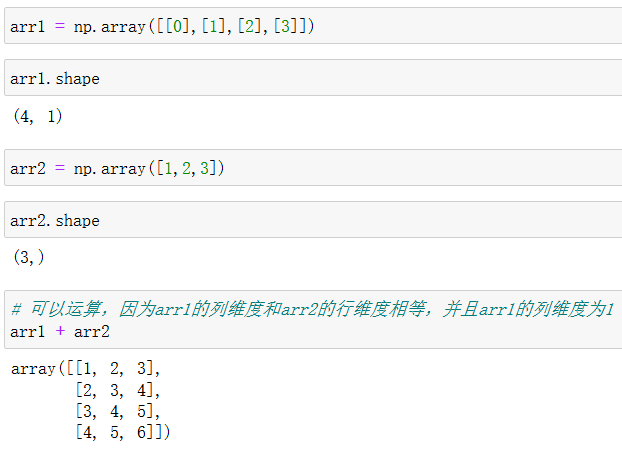

10 矩阵乘法运算
10.1 矩阵和标量的乘法

10.2 矩阵和矩阵/向量的乘法




矩阵与矩阵的运算,使用matmul和dot的效果是一样的。
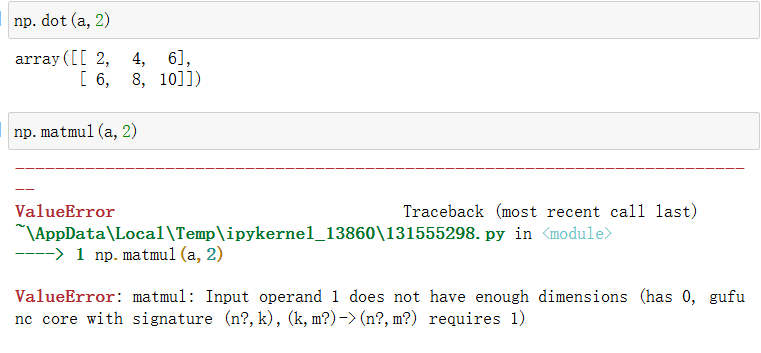
matmul不支持矩阵和标量的运算。
