目录
- 什么是双指针?
- 问题1:移动零
- 问题2:复写零
- 问题3:快乐数
- 问题4:盛最多水的容器
- 问题5:有效三角形个数
- 问题6:查找总价格和为目标值的两个商品(两数之和)
- 问题7:三数之和
- 问题8:四数之和
- 总结
什么是双指针?
双指针算法是一种常见的解决问题的技巧,通常使用两个变量在链表或者数组中进行迭代、遍历,从而达到解决问题的目的。光说理论太抽象,我们来几道题目吧~~
问题1:移动零
力扣链接:移动零

分析一下题目要求: 将给定数组中所有的0移动到数组的末尾,也就是将数组分成两个区域,前半部分是非零元素,后半部分都是零,并且保持非零元素的相对顺序,如示例1,非零元素的顺序:1,3,12,处理之后非零元素的顺序也要是1,3,12,
解题思路:
既然是双指针算法,那我们就定义两个"指针"咯,这里的"指针",我们是指数组下标
定义两个"指针",dest,cur,
dest:已经处理好的区间内,非0元素的最后一个位置
cur:从左往右遍历数组
dest初始为-1,表示刚开始还没非0元素,cur初始为0
在扫描的过程中,一直让数组保持下面这个状态就好了
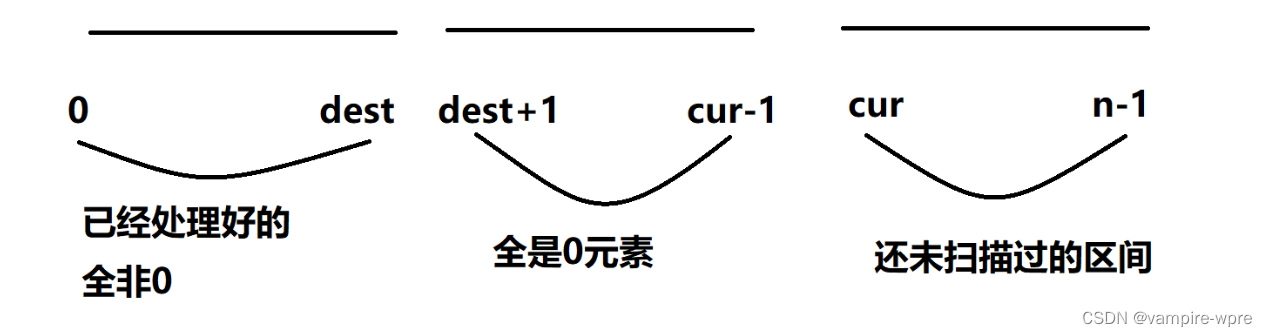
图解:

代码实现:
public void moveZeroes(int[] nums) {//双指针:定义dest和cur,dest初始值为-1//dest的作用:非0元素的最后一个位置,也就是[0,dest]的区间是非0元素//cur的作用:从左往右扫描数组,遍历数组int dest = -1;for (int cur = 0; cur < nums.length; cur++) {if (nums[cur] != 0) {//cur遇到非0元素,先交换dest+1位置和cur位置的元素,再dest++,cur++int tmp = nums[dest + 1];nums[dest + 1] = nums[cur];nums[cur] = tmp; dest++;}}
}
问题2:复写零
力扣链接:复写零

分析一下题目要求: 所谓复写,也就是让我们抄一遍数组的内容,遇到非零的直接抄这个数,遇到零抄两遍零,题目要求我们在原数组上进行操作,也就是说不能重新开辟一个新的数组

解题思路:
先找到最后一个需要被复写的数,然后从后往前进行复写,如果从前往后,后面的数会被覆盖掉。
如何找到最后一个被复写的数?还是利用双指针算法,如图

根据cur位置的值,判断dest向前走一步还是两步,走完判断dest是否到达结束位置(dest是否>=arr.length-1),如果dest没有到达结束位置,则让cur++。重复上面的步骤,当dest到达最后位置时,cur指向的就是最后一个被复写的数,要注意的是,dest的位置可能是arr.length-1,也可能是arr.length,如果dest=arr.length(如下图),需要处理这个边界问题,

处理办法:arr[arr.length - 1] = 0;dest -= 2;cur- -;
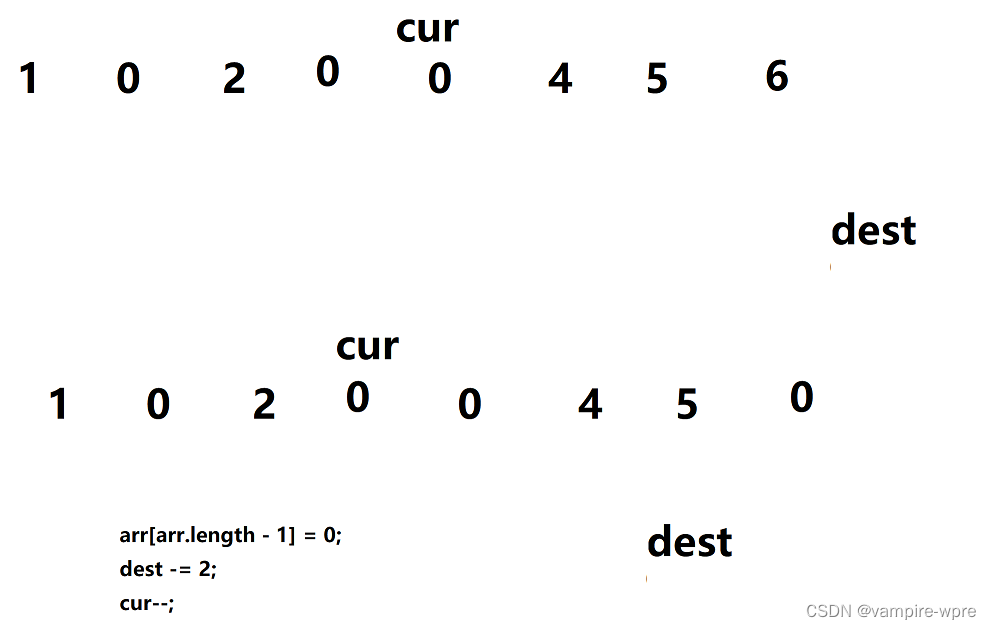
接下来就可以从后往前开始复写了,拿下图举例

代码实现:
public void duplicateZeros(int[] arr) {int cur = 0;//指向最后一个位置int dest = -1;//dest指结果中,最后需要复写的位置,开始时不知道dest在哪,所以-1//先找到最后一个被复写的数while (cur < arr.length) {if (arr[cur] == 0) {dest += 2;} else {dest++;}if (dest >= arr.length - 1) {break;}cur++;}//边界情况,可能出现:最后要复写两个0,第二个0在arr.length这个位置if (dest == arr.length) {arr[arr.length - 1] = 0;dest -= 2;cur--;}while (cur >= 0) {if (arr[cur] != 0) {arr[dest] = arr[cur];dest--;} else {arr[dest--] = 0;arr[dest--] = 0;}cur--;}}
问题3:快乐数
力扣链接:快乐数

题目要求:题目让我们判断给定的数是不是快乐数,快乐数:每次都对这个数进行一次操作(让它的值替换为它每一位的数的平方之和),重复这个操作,判断最终结果是不是变成1或者无限循环变不到1
解题思路:有点类似之前写过的判断链表是否成环,题目说明了结果是1或者无限循环,但是其实1也是无限循环,1重复上述操作结果永远都是1,所以我们可以使用快慢指针的思想,当两个指针相遇时,判断两个指针指向的数是不是1即可(如果不熟悉判断链表是否成环,可以看这篇哦链表OJ)
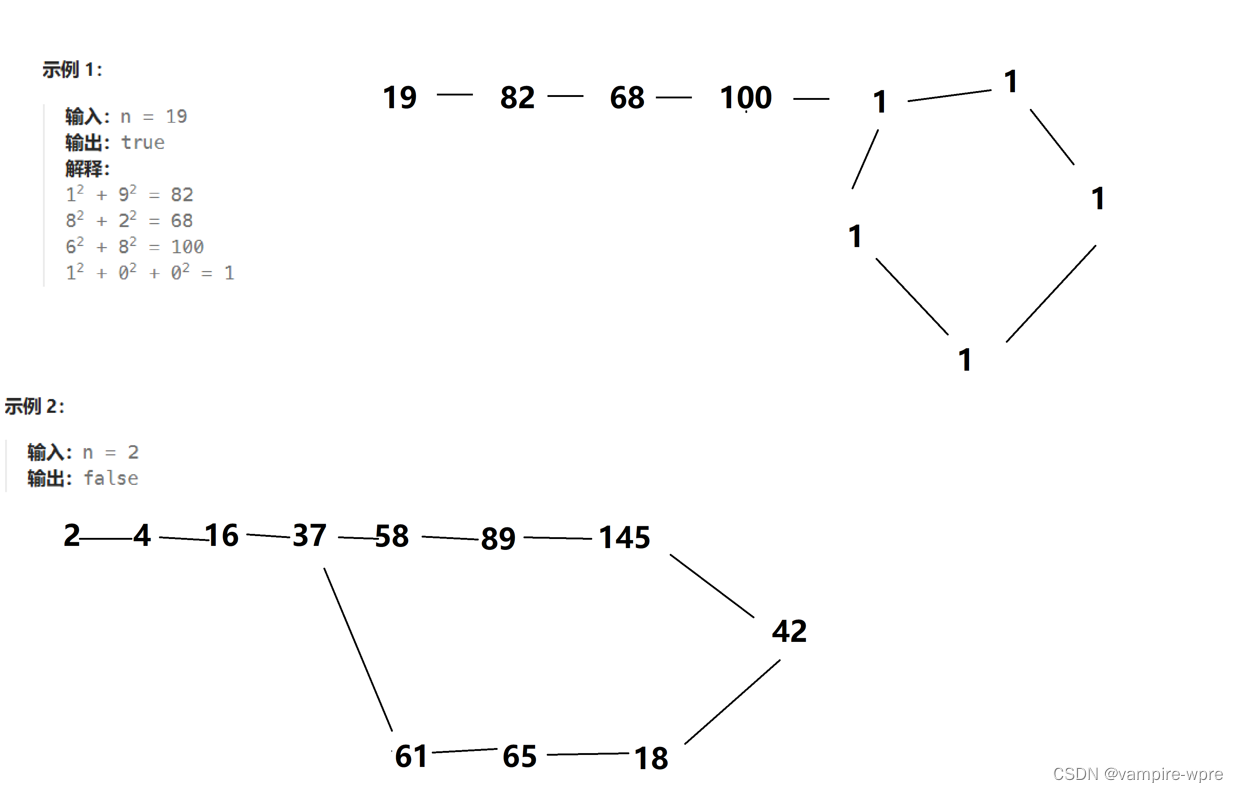
代码实现:
//返回n的每一位的平方之和
public int func(int n) {int sum = 0;while (n != 0) {int t = n % 10;sum += t * t;n /= 10;}return sum;
}public boolean isHappy(int n) {int fast = func(n);int slow = n;while (fast != slow) {slow = func(slow);fast = func(func(fast));}return fast == 1;
}
问题4:盛最多水的容器
力扣链接:盛最多水的容器
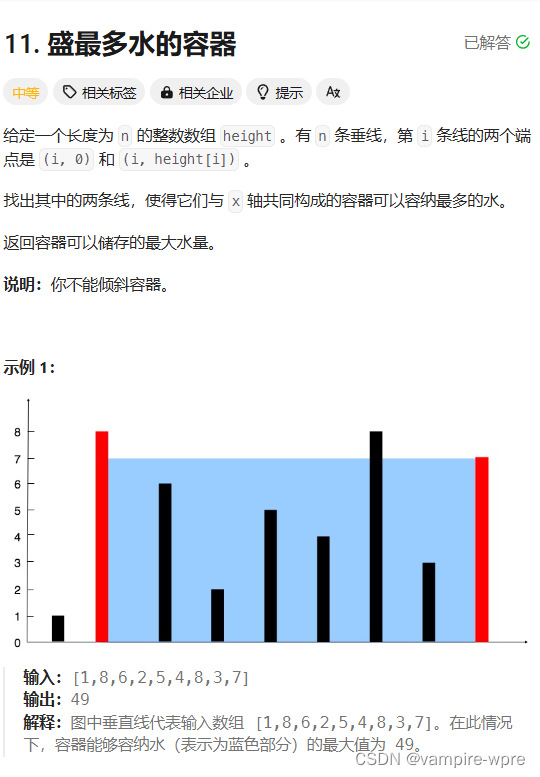
题目要求: 给定了n条垂线,题目要找出两条线,与X轴构成的容器最多能盛水的容积
解题思路: 容积V = h*w,其中,h指高度,也就是两条线的最短的那条,w指宽度
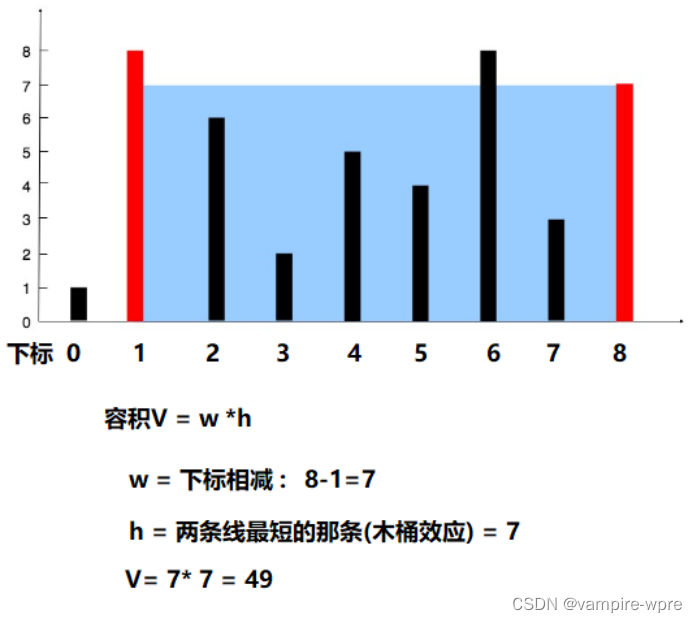
如图:
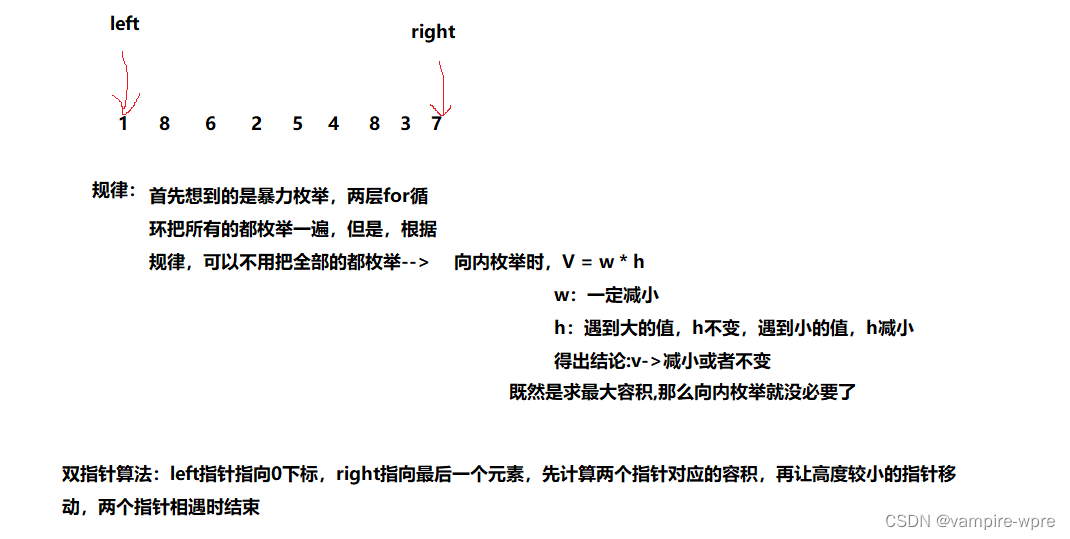
代码实现
public int maxArea(int[] height) {//根据规律:向内枚举时,要么宽度肯定减小,但是高度只能是不变或减小(木桶效应)int left = 0;int right = height.length - 1;int maxV = 0;int V = 0;while (left < right) {V = (right - left) * Math.min(height[left], height[right]);if (V > maxV) {maxV = V;}//让高度小的移动,高度小也叫说明容积小,不符合要求if (height[left] <= height[right]) {left++;} else {right--;}}return maxV;
}
问题5:有效三角形个数
力扣链接:有效三角形个数

题目要求:
给定非负整数数组,在数组中挑3个能组成三角形数,求有几种挑法
解题思路:



代码实现:
public int triangleNumber(int[] nums) {// 利用单调性,使用双指针算法int count = 0;int[] ret = nums;Arrays.sort(ret);// 先排个序int flg = ret.length - 1;//固定好flg,表示最大的数while (flg >= 2) {//固定好flg之后,再利用双指针int left = 0;int right = flg - 1;while (left < right) {if (ret[left] + ret[right] > ret[flg]) {count += (right - left);right--;} else {left++;}}flg--;}return count;}
问题6:查找总价格和为目标值的两个商品(两数之和)
力扣链接:查找总价格和为目标值的两个商品

题目要求: 给定数组和target(题目说明了已经排好序了),求数组中和为target的两个数,以数组的形式返回这两个数即可
解题思路: 定义双指针left,right分别指向第一个和最后一个元素,求两个指针指向的元素之和如果小于target,说明,要大一点!让left++,同理如果大于target,说明要小一点~~,让right–,当两个值等于target,此时可以返回了
代码实现:
public int[] twoSum(int[] price, int target) {int[] ret = new int[2];//返回的数组//定义双指针left,rightint left = 0;int right = price.length - 1;while (left < right) {int sum = price[left] + price[right];if (sum < target) {left++;} else if (sum > target) {right--;} else {ret[0] = price[left];ret[1] = price[right];break;}}return ret;}
问题7:三数之和
力扣链接:三数之和

题目要求:
给定整数数组,判断是否存在相加和为0的三个数,这三个数的下标不能重复,也就是说这三个数下标是不一样的,返回所有的三元组,答案不能是重复的三元组
解题思路:

找到之后left和right继续移动,解决了不漏的问题,能够把所有的三元组都找出来,但是并没有满足题目要求:不能重复,解决办法就是:当找到两个数后,记录left和right的值,left和right跳过重复的数,另外,固定的数a(下标是flg)也要跳过重复的数
代码实现:
public List<List<Integer>> threeSum(int[] nums) {Arrays.sort(nums);//先排序int flg = 0;//固定一个的数List<List<Integer>> ret = new ArrayList<>();// 返回的Listwhile (flg <= nums.length-2) {//双指针算法,left,rightint left = flg + 1;//左指针int right = nums.length - 1;//右指针int a = nums[flg];//双指针找目标值和为-a的两个数if(a>0) {//小优化,大于0了,后面的都是>0的数,肯定找不到-abreak;}//双指针算法,思路和求两数之和一样while (left < right) {if (nums[left] + nums[right] < (-a)) {left++;} else if (nums[left] + nums[right] > (-a)) {right--;} else {List<Integer> list = new ArrayList<>();list.add(a);list.add(nums[left]);list.add(nums[right]);ret.add(list);//// 找到结果之后,left,right跳过重复元素,避免越界int leftNumber = nums[left];int rightNumber = nums[right];while (nums[left] == leftNumber && left < nums.length - 1) {left++;}while (nums[right] == rightNumber && right > 0) {right--;}}}// flg也要跳过重复的元素,flg不能越界while (nums[flg] == a&&(flg <= nums.length-2)) {flg++;}}return ret;}
问题8:四数之和
力扣链接:四数之和

题目要求:
在给定数组中,找出4个和为target的数,这四个数的下标不能重复
解题思路:
明白了两数之和跟三数之和后,四数之和的思路就很简单了,先排序,固定一个数a(最左边或者最右边的数,都是一样的),然后在后面的区间按照三数之和的思路:固定一个数b,按照两数之和找出和为target-a-b的两个数

同样的,left、right、flg1、flg2也要跳过重复的数
代码实现:
public List<List<Integer>> fourSum(int[] nums, int target) {Arrays.sort(nums);List<List<Integer>> ret = new ArrayList<>();// 返回的Listfor (int i = 0; i < nums.length; ) {//固定数afor (int j = i + 1; j < nums.length; ) {//固定数bint left = j + 1;int right = nums.length - 1;long aim = (long) target - (nums[i] + nums[j]);//a+bwhile (left < right) {if (nums[left] + nums[right] < aim) {left++;} else if (nums[left] + nums[right] > aim) {right--;} else {List<Integer> list = new ArrayList<>();list.add(nums[left]);list.add(nums[right]);list.add(nums[i]);list.add(nums[j]);ret.add(list);//处理细节,去重int leftNumber = nums[left];int rightNumber = nums[right];while (nums[left] == leftNumber && left < nums.length - 1) {left++;}while (nums[right] == rightNumber && right > 0) {right--;}}}j++;while ((j < nums.length - 2) && nums[j - 1] == nums[j]) {j++;}}i++;while ((i < nums.length - 3) && nums[i - 1] == nums[i]) {i++;}}return ret;
总结
遇到数组划分问题(按要求将数组分划分几个区域)或者如果数组存在单调性(有序的)时,我们可以考虑双指针算法~~
