前言
iclr24终于可以在openreview上看预印本了
这篇(可能是颠覆之作)文风一眼c re组出品;效果实在太惊艳了,实验相当完善,忍不住写一篇解读分享分享。
TL;DR (overview)
Structured State-Space Model (SSM, S4) 是一个线性时不变系统 ( Linear Time Invariance, LTI), 其参数 (Δ,A,B,C) 是static的,与输入无关,i.e., data independent。 S4虽然在玩具数据集LRA上表现良好,但是在下游任务普遍拉垮。Attention机制的成功arguably可以认为是有data dependent的QKV矩阵来进行交互,这篇的核心思路是让这些参数data dependent,做出了如下的改动:

B: batch size, L: sentence length, D: input dimension, N: RNN hidden dimension
我们可以看到 B,C 的大小从原来的 (D,N) 变成了 (B,L,N) , Δ 的大小由原来的 D 变成了 (B,L,D) ,每个位置的 B,C,Δ 都不相同 (之前是在所有位置共享)。
虽然A没有data dependent, 但是通过state space model的离散化操作之后, (A¯,B¯) 会经过outer product 变成 (B,L,N,D) 的data dependent张量,以一种parameter efficient的方式来达到data dependent的目的。
其余主要改动/贡献如下(技术细节在文末):
(1) 由于SSM的参数data dependent, 此时失去了LTI的性质,不能像之前的S4一样通过FFT来训练了。本文提出了IO-aware的parallel scan(一种memory bounded算子)算法来进行高效训练,降低整体的读写量从而提高wall-time efficiency。上面提到的outer product的参数化方式也对降低整体读写量很有帮助(大致思路是 (A¯,B¯) 在SRAM里面on-the-fly算出来,避免materialization带来的读写开销)
(2) 如果用一个线性层参数化 Δ:R[B×L×D]→R[B×L×D]需要 D[2] 参数。本文提出了一种low-rank projection的参数化方式,可以通过很小的额外参数量来获得较大的提升。最后负责token mixing的SSM只需要很少的参数,绝大多数参数都分给channel mixing了。从MetaFormer的视角来看,token mixing相对channel mixing而言不是重要,所以从这个视角出发的话分配很少的参数是极其合理的。
(3) 以往的SSM经常需要一个output gate来达到很好的效果,如Gated SSM, 这个结构跟gated MLP很像。所以作者干脆把token mixing和channel mixing合二为一,提出了一个新的极简风的Mamba block。(Update: 这跟Gated Attention Unit挺像的)
如下图所示。

实验部分是最让人惊喜的:

Chinchilla scaling laws, 训练长度2048
其中Transformer++指的是带有Rope和SwiGLU的版本(i.e., LLaMa用的)。可以看到之前声称match Transformer performance的model基本上最多也就match一下vanilla transformer的结果 (i.e., 不带rope,如图绿线所示)(吐槽:Hyena是真的辣鸡)

Mamba在8192训练长度上也能match Transformer++的结果

下游任务evaluation,Mamba无情刷榜
技术细节
S4简介
Recommended Reading:
Structured State Spaces for Sequence Modeling (S4)
Simplifying S4
S4的连续微分方程形式(一般也用不着):
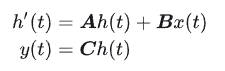
离散形式:
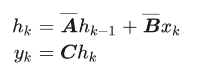
其中最常用到的离散化方法是zero-order hold (ZOH):
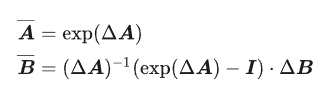
其中 A¯∈R[N×N],B¯∈R[N×1],C∈R[1×N],Δ∈R, N 是SSM hidden state的大小。 需要强调的是 S4用的是Single-input-single-output (SISO), 即对应于每一个输入的维度,都有一套独立的SSM参数 (传统的RNN是MIMO, multiple-input-multiple-output, 很容易混淆)
Parameter-efficient的data dependent参数化方式
上面的S4的参数都是静态的,这肯定不行()所以要弄成data dependent的动态的
这一套的思路由来已久,CV领域的dynamic convolutional,Transformers里面的QKV, LSTM里面的gating都是类似的思想

注意到,对于每个input dimension A只需要N个参数, 因为我们通常会对A做对角化
作者用
![]()
来将 B,C,Δ data dependent化, 其中 Linear d(X) 是把 D维的输入向量 X 经过一个线性层map到 d 维。这里的总参数量大概是 D∗N∗2+D∗D 。 N 即SSM的hidden dimension,一般设的比较小 (e.g., 16),所以 D∗N∗2 部分的参数量是少头,而参数化 sΔ 的 D∗D 是大头(一般至少都是几k维)
所以作者用了一个low-rank projection来降低参数量:
sΔ(X)=LinearD(Linear1(X))
这样总参数量就从 D∗D 降低到了 2D 。
最后作者选择把A设成了data independent,作者给出的解释是反正离散化之后 A¯=exp(ΔA) , Δ 的data dependent能够让整体的 A¯ data dependent。
(PS: 这个解释理由感觉有点牵强,因为如果这样的话, B 也完全可以data independent,靠 Δ 让 B¯ data dependent)
理解参数的含义和功能
step size Δthat represents the resolution of the input
discretization of SSMs is the principled foundation of heuristic gating mechanisms.
这个量跟RNN里的gating有着深刻的联系[1] ,data dependent的 Δ 跟RNN的forget gate的功能类似

经典的RNN gating可以理解成SSM离散化的一个特例。
而 B和C 所起到的功能类似于写(进RNN的memory)和读(取RNN的memory)。所以data dependent的B/C的功能跟RNN的input/output gate类似。
A的作用其实有点尴尬,因为 Δ 已经有点遗忘门的意思了。但注意到对于每个input维度来说, Δ 只是一个标量,而 A∈R[N×1] ,也就是说对应这个维度的SSM来说,A在每个hidden state维度上的作用可以不相同,起到multi-scale/fine-grained gating的作用,这也是LSTM网络里面用element-wise product的原因(i.e., forget gate是跟隐藏层维度相同的一个向量,而不仅仅是一个标量)
这篇文章所强调的selectivity无非就是传统门控RNN经典的思想。。。属于是文艺复兴/新瓶装旧酒
Recommended Reading:
十分推荐一篇鞭辟入里的文章
Written Memories: Understanding, Deriving and Extending the LSTM
IO-aware Parallel Scan
因为现在的参数都是data dependent了,所以不再是LTI,也就失去了卷积的性质,不能用FFT来进行高效训练了。
不过这也不是什么问题,之前的S5已经指出了data dependent的SSM可以用parallel scan来进行训练。不过parallel scan依然是memory bounded的操作,对于SSM这种每个input维度对应一个RNN的SISO模型来说,总共有效的RNN hidden state可以理解成 N∗D ,所以实现的不好的话很容易比较慢。S5为了避免这个问题,选择了MIMO的方式并且降低总体的维度。Mamba选择迎难而上,利用kernel fusion, recomputation的经典优化思想来硬上 (PS: 很好很c re组)
一般的实现会提前先把大小为 (B,L,D,N) 的 A¯,B¯ 先算出来,然后把它们从HBM (high-bandwith memory, or GPU memopry) 读到SRAM, 然后调用scan算子算出 (B,L,D,N) 的output,写到HBM里面。再开一个kernel把 (B,L,D,N) 的output以及 (B,L,N) 的C读进来,multiply and sum with C得到最后的 (B,L,N) output 。整个过程的读写是 O(BLDN) 。本文提出的方法:
- 把 (Δ,A,B,C) 读到SRAM里面,总共大小是 O(SLN+DN)
- 在SRAM里面做离散化,得到 (B,L,D,N) 的 A¯,B¯
- 在SRAM里面做scan,得到 (B,L,D,N) 的 output
- multiply and sum with C,得到最后的 (B,L,D) output 写入HBM
整个过程的总读写量是 O(BLN) ,比之前省了O(N)。 backward的时候就把 A¯,B¯ 重算一遍,类似于flashattn重算attention分数矩阵的思想。只要重算的时间比读 O(BLDN) 快就算胜利
We benchmark the speed of the SSM scan operation (N = 16), as well as the end-to-end inference throughput of Mamba, in Figure 8. Our efficient SSM scan is faster than the best attention implementation that we know of (FlashAttention-2 (Dao, 2023)) beyond sequence length 2K, and up to 20-40× faster than a standard scan implementation in PyTorch.

IO-aware的实现比naive实现快很多倍;(flash)scan 在输入长度2k的时候就开始比flashattention快了, 之后越长越快。同时scan也比long convolution (w/ FFT)快,再次给long convolution模型敲上丧钟(本来long conv模型inference的时候就很笨了,训练还慢就更...
Token mixing+Channel Mixing合二为一

之前的SSM模型要work,都会加上output gating,之后再过个线性层channel mixing,如上图的最左边所示。这两个部分跟Gated MLP(上图中间)右边的支路和最上面的channel mixing是一样的。所以SSM层如果跟Gated MLP叠的话,难免会感觉有点冗余,所以作者干脆把两个合二为一,把token mixing层和channel mixing层合二为一 (PS: 估计会有很深远的影响),并且做work了。
现在的新的Mamba block有 3ED[2] 个参数(E是FFN扩展的倍数,一般transformer里面E是扩大四倍)。如果E=4,那么正好对应于一个 12D[2] 也就是一层transformer layer的总参数量。但可能是因为RNN比较吃层数(也很好形象理解,RNN是比较local的模型,所以需要叠深度来换一层attend到的广度),所以作者选择E=2,一层包含两个这样的Mamda block。
消融实验

对不同参数data dependent的敏感性
上文提到 Δ 的作用类似遗忘门,而遗忘门毫无疑问是LSTM里面最重要的门[2],所以这个消融实验结果发现 Δ data dependent带来的收益效果最大就一点都令人惊讶啦
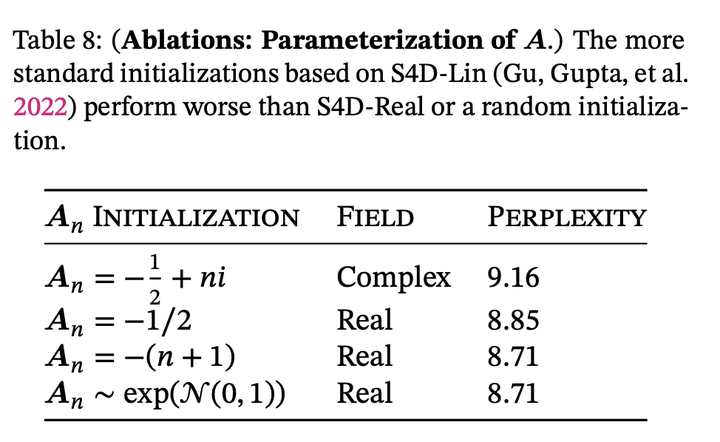
A用实数还是虚数,以及A的参数化方式
这篇发现complex的decay rate不如real;跟rwkv作者的观点一致。之前的data independent的ssm模型发现虚数挺重要的;这里的实验现象相左的可能原因是因为data dependent的ssm表达能力本身就足够强了,不需要复数带来的额外表达能力;而之前data independent的ssm如果不用虚数来对角化A,表达能力相当受限

\Delta参数化时使用的low-rank的rank size
之前提到了参数化 Δ 的时候用low-rank来降低ssm部分的参数。其中一个可能的深意是 Metaformer框架认为token mixing远不如channel mixing重要,所以与其把参数分配给token mixing,不如把参数分配给channel mixing。最上面的那一行是data independent;rank=1的时候可以发现就已经有提升了,证明了data dependent的有效性;之后接着加参数也有提升 (但不确定如果多出来的参数加到channel mixing里面会不会更好)

SSM hidden size的影响,上面是data independent, 下面是data dependent
我们可以看到data independent的时候,增大SSM hidden state size的帮助很小,反而增大了很多计算量;而data dependent的时候,增大SSM hidden state size的收益大得多,体现了selectivity的优势

这个表体现了把token mixing和channel mixing合二为一成一个单独的Mamba层的好处 (PS: 似乎只有对这个模型有效,对其他模型反向提升)。
总结
把经典LSTM选择性的思想引入了SSM,极致的implementation优化,solid的全方位的实验,惊艳的实验效果,可能彻底打破大家对RNN的印象
参考
- ^https://arxiv.org/abs/1804.11188
- ^https://arxiv.org/abs/1804.04849
附赠
【一】上千篇CVPR、ICCV顶会论文
【二】动手学习深度学习、花书、西瓜书等AI必读书籍
【三】机器学习算法+深度学习神经网络基础教程
【四】OpenCV、Pytorch、YOLO等主流框架算法实战教程
➤ 添加助理自取:

➤ 还可咨询论文辅导❤【毕业论文、SCI、CCF、中文核心、El会议】评职称、研博升学、本升海外学府!