摘要:
1,跳表的介绍
2,跳表节点的插入
3,跳表的查询
4,跳表节点的删除
1,跳表的介绍
我们知道如果数组是有序的,查询的时候可以使用二分法进行查询,时间复杂度可以降到 O(logn) 。但如果链表是有序的,我们仍然需要从前往后一个个查找,这样显然很慢,这个时候我们可以使用跳表(Skip list)。
跳表(Skip list)又称跳跃表,它是一种随机化的数据结构,因为节点从第几层开始插入是随机的。
跳表是一种可以进行二分查找的有序链表,它也是多层链表,每一层链表都是有序的,最下面一层是原始链表,包含所有数据,从下往上每层节点个数逐渐减少。
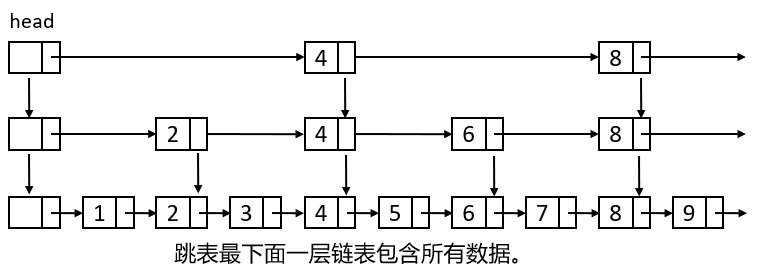
跳表的特性:
1,一个跳表有若干层链表组成;
2,每一层链表都是有序的;
3,跳表最下面一层的链表包含所有数据;
4,如果一个元素出现在某一次层,那么该层下面的所有层都必须包含该元素;
5,上一层的元素指向下层的元素必须是相同的;
6,头指针 head 指向最上面一层的第一个元素;
2,跳表节点的插入
如果是单链表只需要找出待插入节点的前一个节点即可,但在跳表中不光要插入到原始链表中,在他上面的某些层也有可能需要插入,实现方式有随机性和确定性两种选择,其中随机性一般比较常见。
比如要在跳表中插入一个元素,可以随机生成一个数字 level ,从 level 层往下每层都要插入。所以跳表中节点不光有 next 属性,还有 down 属性,down 是指向下一个节点的指针,先来看下跳表的节点类。
Java代码:
// 跳表的节点类。
public class SkipListNode {// 跳表节点的值,在实际应用中节点类可以加个泛型,这里为了方便介绍,直接使用 int 类型。public int val;public SkipListNode next;// 指向后面一个节点。public SkipListNode down;// 指向下面一层的相同节点。public SkipListNode(int val, SkipListNode next) {this.val = val;this.next = next;}
}C++代码:
// 跳表的节点类。
struct SkipListNode {// 跳表节点的值,在实际应用中节点类可以加个泛型,这里为了方便介绍,直接使用 int 类型。int val = 0;SkipListNode *next = nullptr;// 指向后面一个节点。SkipListNode *down = nullptr;// 指向下面一层的相同节点。SkipListNode(int x, SkipListNode *n) : val(x), next(n) {}
};在跳表中还需要定义一个最大值 MAX_LEVEL ,就是跳表的最大层级数,跳表的最大层不能超过这个值。
我们再来看下索引层级的随机函数,他主要用于在插入节点的时候从第几层开始插入,他是随机的,越往上机率越小,这也符合跳表的特性,越往上节点越少,最大值不能超过 MAX_LEVEL 。
Java代码:
// 索引层级随机函数。
private int randLevel() {int level = 1;// 1 的概率是0.5,2的概率是0.25,3的概率是0.125,4的概率是0.0625,……// Math.random()每次会生成一个 0 到 1 之间的随机数while (Math.random() < 0.5f && level < MAX_LEVEL)level++;return level;
}C++代码:
// 索引层级随机函数。
int randLevel() {int level = 1;srand(time(NULL));// (rand() % 100)每次会生成一个 0 到 99 之间的随机数while ((rand() % 100) < 50 && level < MAX_LEVEL)level++;return level;
}在跳表中每一层都有一个头节点,头节点不存储任何数据,其中 head 是最上面一层的头节点,跳表的插入,删除以及查找都是从头节点开始的,如果想要获取下面一层的头节点,可以通过 head.down 获取。跳表的插入总共分为 3 步:
第一步:在跳表节点插入之前先判断上面的层级有没有创建,如果没有创建,需要先创建,如下图所示。
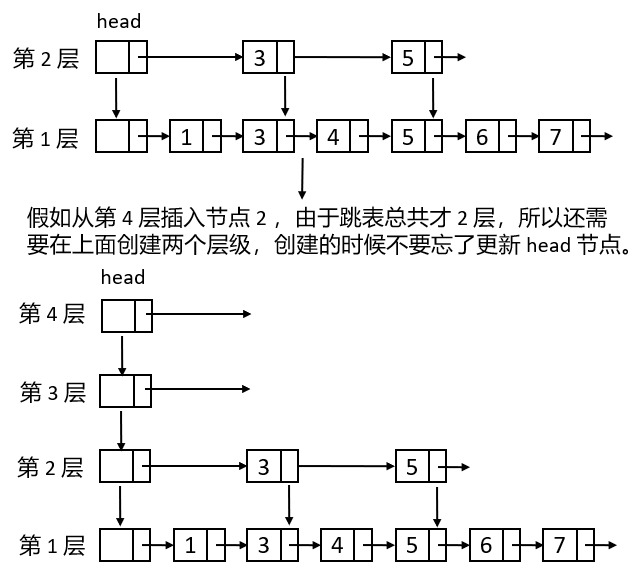
第二步:如果创建了层级或者插入的层级小于跳表的层数,需要找到每一层待插入节点的前一个节点,如下图所示。
