



































 选择题1参考程序:
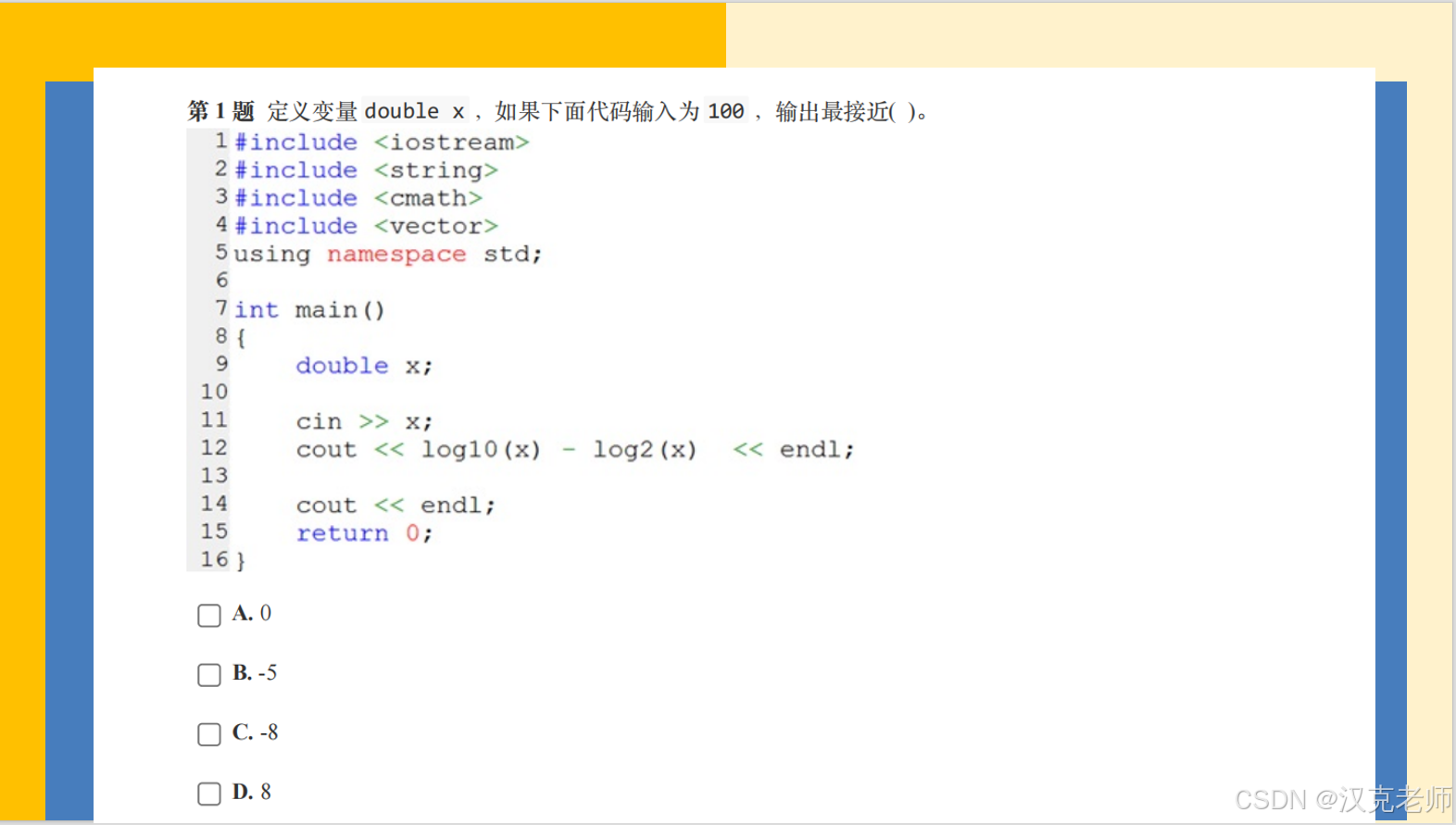
选择题1参考程序:
#include <iostream>
#include <string>
#include <cmath>
#include <vector>
using namespace std;int main(){double x;cin >> x;cout << log10(x) - log2(x) << endl;cout << endl;return 0;
}
选择题2参考程序:
#include <iostream>
#include <climits> // 提供 INT_MAX
using namespace std;const int MAX_N = 210; // 最大石子数量(可根据题目要求调整)
const int MAX_F = INT_MAX / 2; // 避免加法溢出int s[MAX_N]; // 前缀和数组
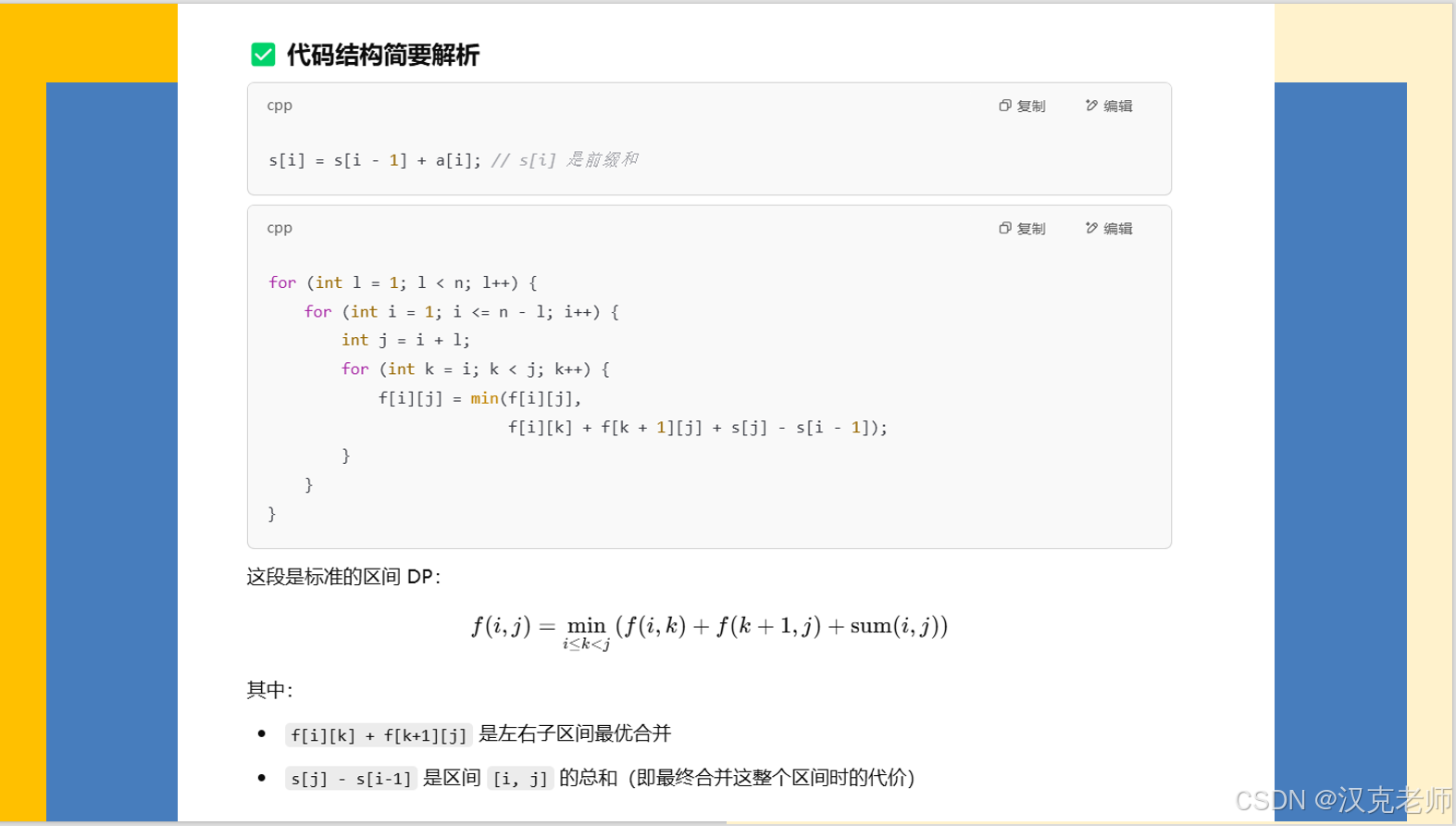
int f[MAX_N][MAX_N]; // DP数组,f[i][j] 表示合并第 i 到 j 堆石子的最小代价int stone_merge(int n, int a[]) {// 构建前缀和数组 s,使我们能快速计算任意区间 [i, j] 的石子总和for (int i = 1; i <= n; i++) {s[i] = s[i - 1] + a[i];}// 初始化 DP 表for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {if (i == j) f[i][j] = 0; // 合并一个堆,代价为 0else f[i][j] = MAX_F; // 其他值初始化为较大值}}// 枚举区间长度(从2开始)for (int l = 1; l < n; l++) {for (int i = 1; i <= n - l; i++) {int j = i + l; // 区间终点for (int k = i; k < j; k++) {// 状态转移:尝试把区间 [i,j] 拆成 [i,k] 和 [k+1,j] 两部分合并f[i][j] = min(f[i][j], f[i][k] + f[k + 1][j] + s[j] - s[i - 1]);}}}return f[1][n]; // 返回合并整个区间 [1,n] 的最小代价
}int main() {int n;int a[MAX_N];// 输入石子堆数量cout << "请输入石子堆数量 n:" << endl;cin >> n;// 输入每堆石子的数量,数组从下标 1 开始使用cout << "请输入 " << n << " 个石子的数量:" << endl;for (int i = 1; i <= n; i++) {cin >> a[i];}// 调用函数并输出结果int result = stone_merge(n, a);cout << "最小合并代价为:" << result << endl;return 0;
}选择题3参考程序:
#include <iostream>
#include <algorithm> // 提供 max 函数
using namespace std;const int MAX_N = 2023;
int a[MAX_N]; // 存储输入序列
int f[MAX_N]; // f[i] 表示以 a[i] 结尾的最长上升子序列长度int main() {int n; // 序列长度int i, j; // 循环变量int ans = -1; // 最终最长子序列的长度// 读入序列长度cout << "请输入序列长度 n:" << endl;cin >> n;// 读入序列元素,从下标 1 开始cout << "请输入 " << n << " 个整数:" << endl;for (i = 1; i <= n; i++) {cin >> a[i];f[i] = 1; // 每个元素至少可以构成一个长度为1的子序列}// 动态规划求解最长上升子序列长度for (i = 1; i <= n; i++) {for (j = 1; j < i; j++) {if (a[j] < a[i]) {f[i] = max(f[i], f[j] + 1);}}}// 输出每个位置的 LIS 长度,并求最大值cout << "每个位置以它结尾的LIS长度:" << endl;for (i = 1; i <= n; i++) {cout << f[i] << " ";ans = max(ans, f[i]);}cout << endl;// 输出最终结果:最长上升子序列长度cout << "最长上升子序列的长度为:" << ans << endl;return 0;
}