十种网络推广的方法_庆阳宁县疫情_广州seo优化效果_营销网站推荐

涉及到二叉树的构造，无论普通二叉树还是二叉搜索树一定前序，都是先构造中节点。
求普通二叉树的属性，一般是后序，一般要通过递归函数的返回值做计算。
求二叉搜索树的属性，一定是中序了，要不白瞎了有序性了。

1、二叉树的递归遍历

// 前序遍历·递归·LC144_二叉树的前序遍历
class Solution {public List<Integer> preorderTraversal(TreeNode root) {List<Integer> result = new ArrayList<Integer>();preorder(root, result);return result;}public void preorder(TreeNode root, List<Integer> result) {if (root == null) {return;}result.add(root.val);preorder(root.left, result);preorder(root.right, result);}
}
// 中序遍历·递归·LC94_二叉树的中序遍历
class Solution {public List<Integer> inorderTraversal(TreeNode root) {List<Integer> res = new ArrayList<>();inorder(root, res);return res;}void inorder(TreeNode root, List<Integer> list) {if (root == null) {return;}inorder(root.left, list);list.add(root.val);             // 注意这一句inorder(root.right, list);}
}
// 后序遍历·递归·LC145_二叉树的后序遍历
class Solution {public List<Integer> postorderTraversal(TreeNode root) {List<Integer> res = new ArrayList<>();postorder(root, res);return res;}void postorder(TreeNode root, List<Integer> list) {if (root == null) {return;}postorder(root.left, list);postorder(root.right, list);list.add(root.val);             // 注意这一句}
}

2、二叉树的迭代遍历（非递归）

递归的实现就是：每一次递归调用都会把函数的局部变量、参数值和返回地址等压入调用栈中，然后递归返回的时候，从栈顶弹出上一次递归的各项参数，所以这就是递归为什么可以返回上一层位置的原因。

2.1 前序遍历

前序遍历是根左右，每次先处理的是中间节点，那么先将根节点放入栈中，然后将右孩子加入栈，再加入左孩子。为什么要先加入右孩子，再加入左孩子呢？因为这样出栈的时候才是中左右的顺序。

class Solution {public List<Integer> preorderTraversal(TreeNode root) {List<Integer> result = new ArrayList<>();if (root == null){return result;}Stack<TreeNode> stack = new Stack<>();stack.push(root);while (!stack.isEmpty()){TreeNode node = stack.pop();result.add(node.val);if (node.right != null){stack.push(node.right);}if (node.left != null){stack.push(node.left);}}return result;}
}

2.2 中序遍历

中序遍历是左根右，先访问的是二叉树顶部的节点，然后一层一层向下访问，直到到达树左面的最底部，再开始处理节点（也就是在把节点的数值放进result数组中），这就造成了处理顺序和访问顺序是不一致的。那么在使用迭代法写中序遍历，就需要借用指针的遍历来帮助访问节点，栈则用来处理节点上的元素。

class Solution {public List<Integer> inorderTraversal(TreeNode root) {List<Integer> result = new ArrayList<>();if (root == null){return result;}Stack<TreeNode> stack = new Stack<>();TreeNode cur = root;while (cur != null || !stack.isEmpty()){if (cur != null){stack.push(cur);cur = cur.left;}else{cur = stack.pop();result.add(cur.val);cur = cur.right;}}return result;}
}

2.3 后序遍历

后序遍历是左右中，那么我们只需要调整一下先序遍历的代码顺序，就变成中右左的遍历顺序，然后在反转result数组，输出的结果顺序就是左右中了，如下图：

所以后序遍历只需要前序遍历的代码稍作修改就可以了，代码如下：

// 后序遍历顺序 左-右-中 入栈顺序：中-左-右 出栈顺序：中-右-左， 最后翻转结果
class Solution {public List<Integer> postorderTraversal(TreeNode root) {List<Integer> result = new ArrayList<>();if (root == null){return result;}Stack<TreeNode> stack = new Stack<>();stack.push(root);while (!stack.isEmpty()){TreeNode node = stack.pop();result.add(node.val);if (node.left != null){stack.push(node.left);}if (node.right != null){stack.push(node.right);}}Collections.reverse(result);return result;}
}

3、二叉树的层序遍历

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {List<List<Integer>> resList = new ArrayList<List<Integer>>();public List<List<Integer>> levelOrder(TreeNode root) {fun(root,0);return resList;}/*** 整体逻辑就是：当reslist.size < deep时，那就创建list* 等于或者大于时，就该往相应的list里面添加元素了。* @param root* @param deep*/private void fun(TreeNode root,int deep) {//思路：每一层对应一个list,最后的结果是一个大的listif (root == null) return ;deep++;  //代表当前在第几层if (resList.size() < deep){//当层级增加时，存放每层元素的集合数也增加，即当前在第几层那么reslist里面就有几个listList<Integer> list = new ArrayList<Integer>();resList.add(list);}resList.get(deep -1).add(root.val);fun(root.left,deep);fun(root.right,deep);}//队列实现public List<List<Integer>> levelOrder1(TreeNode root) {List<List<Integer>> resList = new ArrayList<List<Integer>>();if(root == null)return resList;Queue<TreeNode> que = new LinkedList<TreeNode>();que.offer(root); //队列尾部插入元素while (!que.isEmpty()){List<Integer> list = new ArrayList<Integer>();int len  = que.size();while (len > 0){TreeNode tmpNode = que.poll();list.add(tmpNode.val);if (tmpNode.left !=null)que.offer(tmpNode.left);if (tmpNode.right != null)que.offer(tmpNode.right);len--;}resList.add(list);}return resList;}}

3.1 二叉树的层序遍历II

给定一个二叉树，返回其节点值自底向上的层次遍历。（即按从叶子节点所在层到根节点所在的层，逐层从左向右遍历）,相对于二叉树的层序遍历，就是最后把result数组反转一下就可以了。

3.2 二叉树的右视图

给定一棵二叉树，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

思路：层序遍历，遍历每一层的最后一个节点

public class Case199 {//递归public List<Integer> rightSideView(TreeNode root) {List<Integer> resList = new ArrayList<>();fun(root,0,resList);return resList;}private void fun(TreeNode root,int deep,List<Integer>resList) {if (root == null)return;if (deep == resList.size()){ //这个深度首次达到resList.add(root.val);}fun(root.right,deep + 1,resList);fun(root.left,deep + 1,resList); //这个妙啊！！}//层序遍历，每次返回每层的最后一个节点public List<Integer> rightSideView1(TreeNode root) {Queue<TreeNode> que = new LinkedList<>();List<Integer> list = new ArrayList<>();if (root == null) return list;que.offer(root);while (!que.isEmpty()) {int len = que.size();while (len > 0){TreeNode tmp = que.poll();if (tmp.left != null) que.offer(tmp.left);if (tmp.right != null) que.offer(tmp.right);len--;if (len == 0)list.add(tmp.val);}}return list;}
}

3.3 二叉树的层平均值

给定一个非空二叉树, 返回一个由每层节点平均值组成的数组。

public class Case637 {public List<Double> averageOfLevels(TreeNode root) {List<Double> list = new ArrayList<>();if (root == null)return list;Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);while (!queue.isEmpty()){int len = queue.size();Double sum = 0.0;while (len > 0){TreeNode tem = queue.poll();sum += tem.val;if (tem.left !=null)queue.offer(tem.left);if (tem.right != null)queue.offer(tem.right);len--;if (len == 0){Double res = sum / len;list.add(res);}}}return list;}
}

3.4 N叉树的层序遍历

给定一个 N 叉树，返回其节点值的层序遍历。 (即从左到右，逐层遍历)。例如，给定一个 3叉树 :

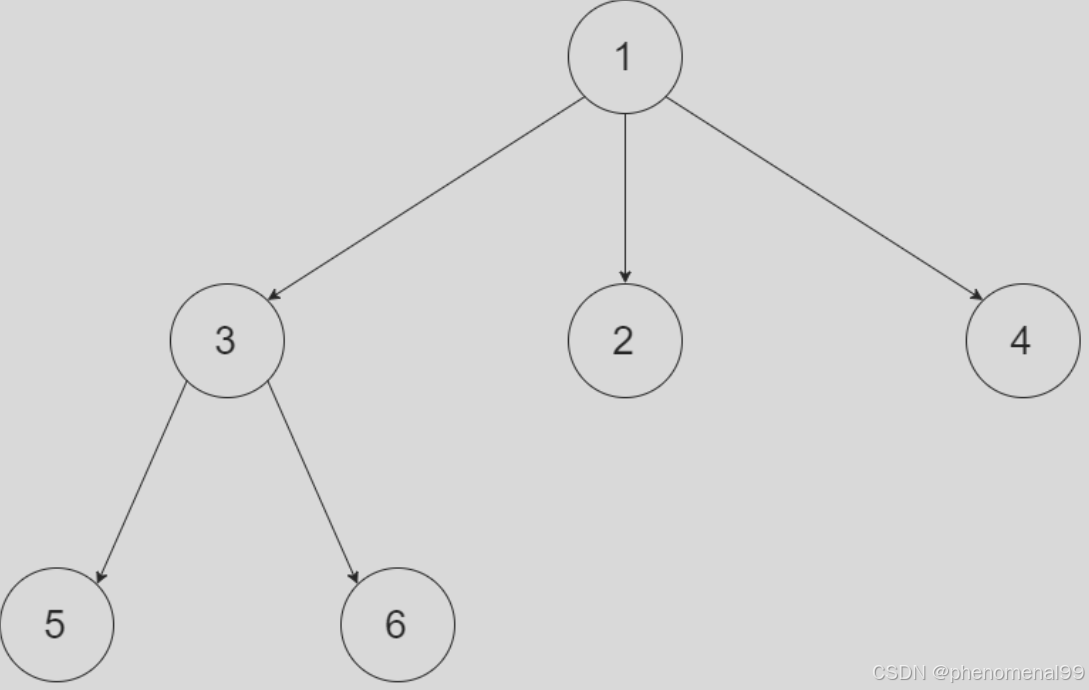
返回其层序遍历:[ [1], [3,2,4], [5,6] ]

/*
// Definition for a Node.
class Node {public int val;public List<Node> children;public Node() {}public Node(int _val) {val = _val;}public Node(int _val, List<Node> _children) {val = _val;children = _children;}
};
*/
public class Case429 {public List<List<Integer>> levelOrder(Node root) {List<List<Integer>> res = new ArrayList<>();if (root == null ){return res;}Queue<Node> queue = new LinkedList<>();queue.offer(root);while (!queue.isEmpty()){List<Integer> list = new ArrayList<>();int len  = queue.size();while (len > 0){Node p = queue.poll();list.add(p.val);if (p.children != null){for (Node child : p.children) {queue.offer(child);}}len--;}res.add(list);}return res;}
}

3.5 在每个树行中找最大值

public class Case515 {/*** 给定一棵二叉树的根节点 root ，请找出该二叉树中每一层的最大值。* @param root* @return*/public List<Integer> largestValues(TreeNode root) {List<Integer> res = new ArrayList<>();Queue<TreeNode> queue = new LinkedList<>();if (root == null) return res;queue.offer(root);while (!queue.isEmpty()) {int len = queue.size();int max = Integer.MIN_VALUE;for (int i = 0; i < len; i++) {TreeNode p = queue.poll();max = Math.max(p.val, max);if (p.left != null)queue.offer(p.left);if (p.right != null)queue.offer(p.right);}res.add(max);}return res;}
}

3.6 填充每个节点的下一个右侧节点指针

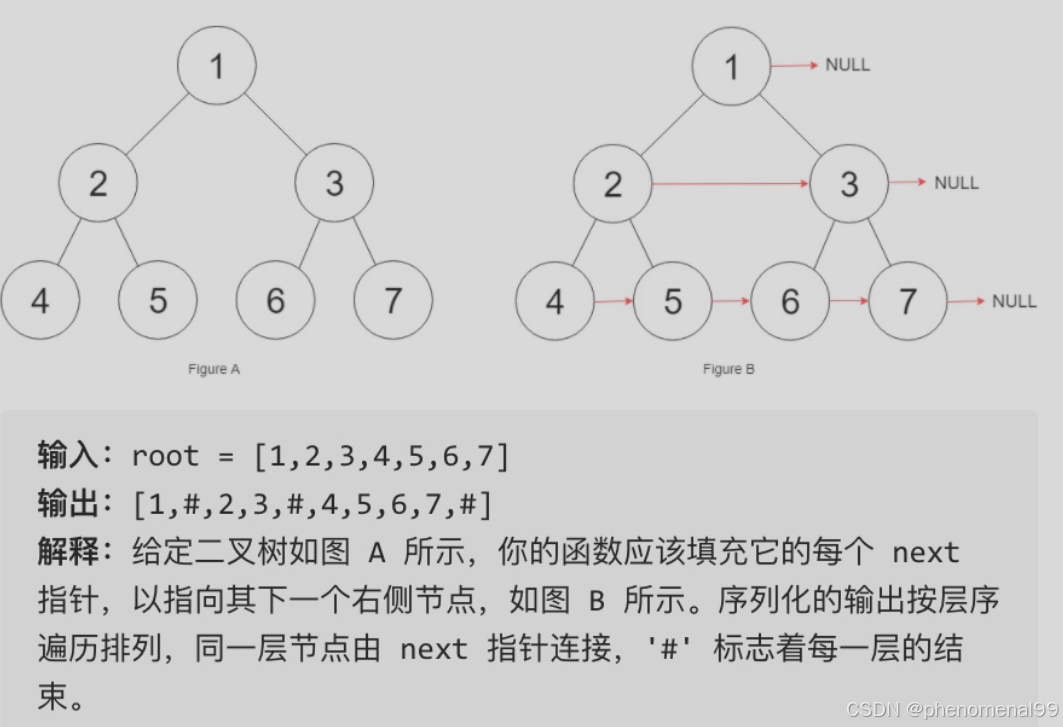
public class Case116 {public Pnode connect(Pnode root) {if (root == null) return null;Queue<Pnode> queue = new LinkedList<Pnode>();queue.offer(root);while (!queue.isEmpty()){int len = queue.size();while (len > 0){Pnode tem = queue.poll();len--;if (len == 0){tem.next = null;}else {tem.next = queue.peek();}if (tem.left != null)queue.offer(tem.left);if (tem.right != null)queue.offer(tem.right);}}return root;}
}

3.7 填充每个节点的下一个右侧节点指针II

与上题一样

3.8 二叉树的最大深度

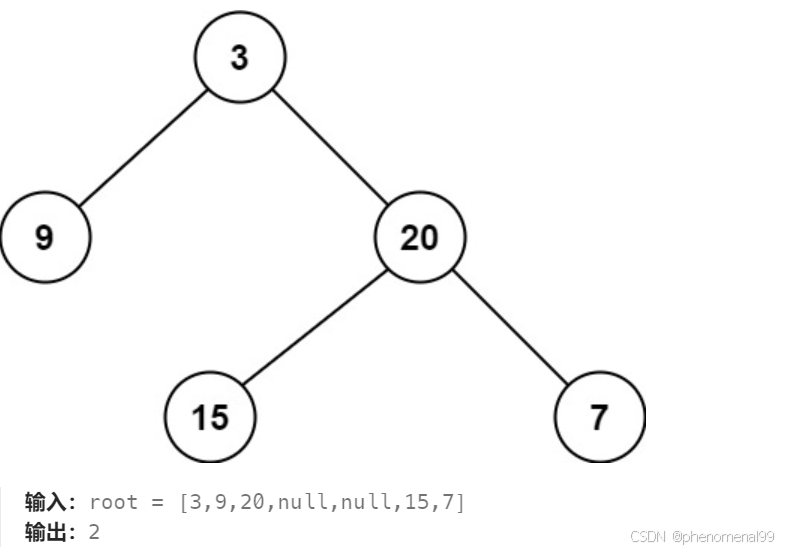
给定一个二叉树，找出其最大深度。二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。说明: 叶子节点是指没有子节点的节点。

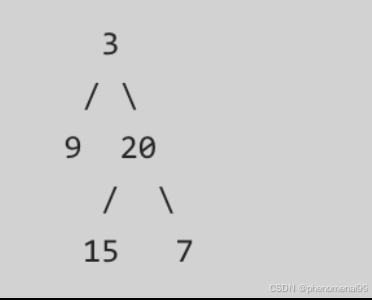
返回它的最大深度 3 。

使用迭代法的话，使用层序遍历是最为合适的，因为最大的深度就是二叉树的层数，和层序遍历的方式极其吻合。在二叉树中，一层一层的来遍历二叉树，记录一下遍历的层数就是二叉树的深度，如图所示：

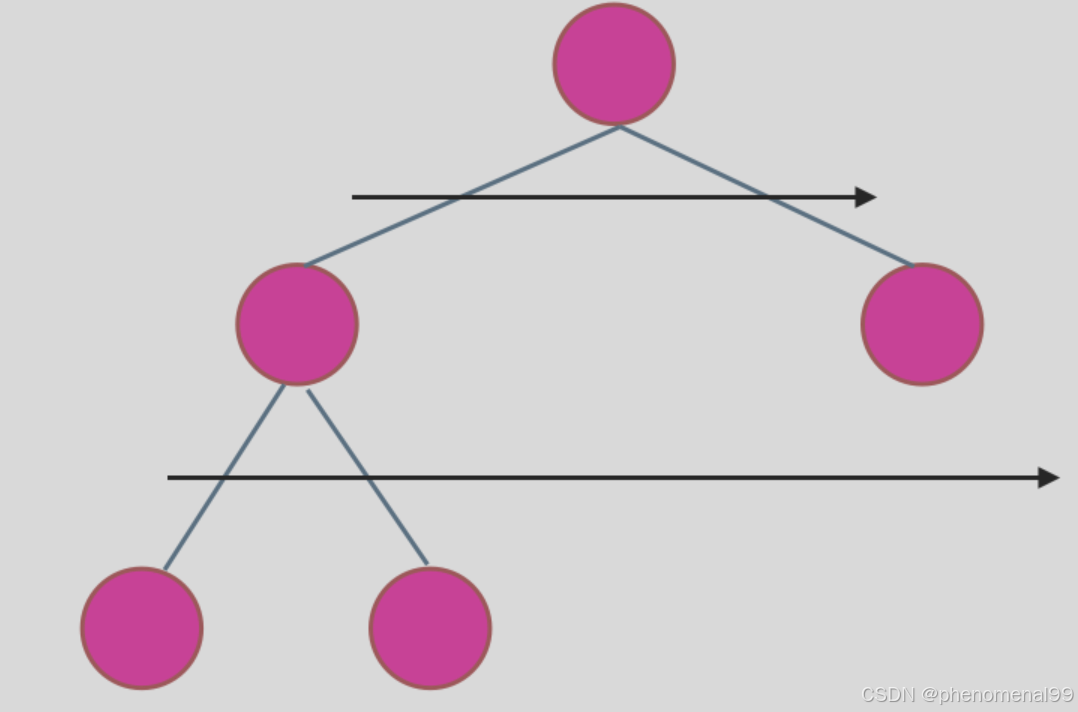
class Solution {public int maxDepth(TreeNode root) {if (root == null)   return 0;Queue<TreeNode> que = new LinkedList<>();que.offer(root);int depth = 0;while (!que.isEmpty()){int len = que.size();while (len > 0){TreeNode node = que.poll();if (node.left != null)  que.offer(node.left);if (node.right != null) que.offer(node.right);len--;}depth++;}return depth;}//递归public int maxDepth(TreeNode root) {if (root == null)return 0;int lDepth = maxDepth(root.left);int rDepth = maxDepth(root.right);int max = Math.max(lDepth,rDepth) + 1;return max;}
}

3.9 二叉树的最小深度

public class Case111 {/*** 与求最大深度还不一样，* @param root* @return*/public int minDepth(TreeNode root) {if(root == null) return 0;int m1 = minDepth(root.left);int m2 = minDepth(root.right);//1.如果左孩子和右孩子有为空的情况，直接返回m1+m2+1//2.如果都不为空，返回较小深度+1return root.left == null || root.right == null ? m1 + m2 + 1 : Math.min(m1,m2) + 1;}// 层序遍历public int minDepth1(TreeNode root){if (root == null) return 0;Queue<TreeNode>queue = new LinkedList<>();queue.offer(root);int depth = 0;while (!queue.isEmpty()){depth++; //每遍历完一层深度+1int len = queue.size();while (len > 0) {TreeNode p = queue.poll();if (p.left == null && p.right == null) return depth; //到达叶子节点了if (p.left != null) queue.offer(p.left);if (p.right != null) queue.offer(p.right);len--;}}return depth;}
}

4、反转二叉树

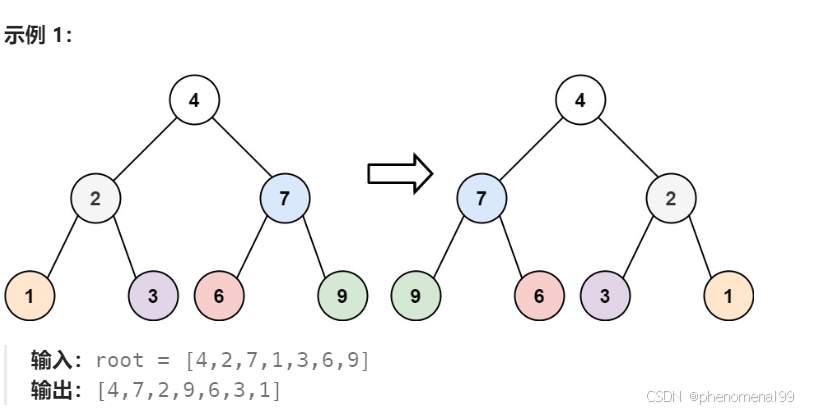
给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

public class Case226 {public TreeNode invertTree(TreeNode root) {if (root == null) return null;Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);while (!queue.isEmpty()){int len = queue.size();while (len > 0){TreeNode p = queue.poll();swap(p);if (p.left != null)queue.offer(p.left) ;if (p.right != null)queue.offer(p.right);len--;}}return root;}private void swap(TreeNode p) {TreeNode temp = p.left;p.left = p.right;p.right = temp;}//递归public TreeNode invertTree1(TreeNode root) {if (root == null) return null;invertTree1(root.left);invertTree1(root.right);swap(root);return root;}

5、对称二叉树

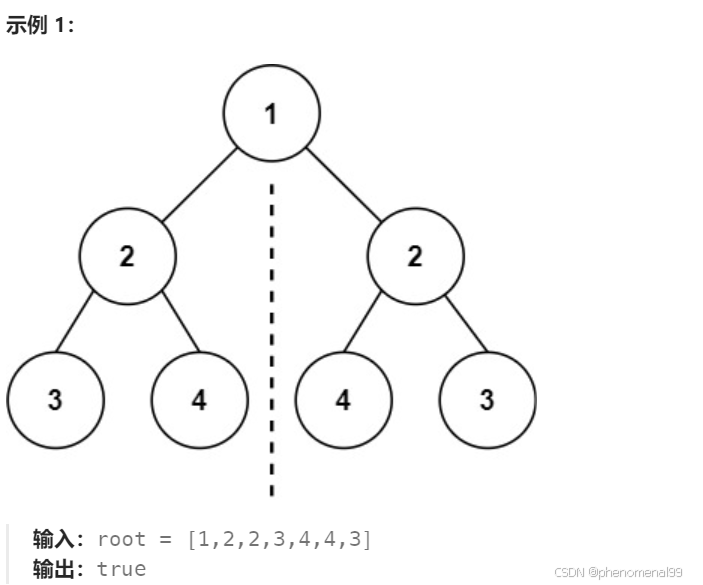
给定一个二叉树，检查它是否是镜像对称的。

/*** 简单题并不简单* 按照普通层序遍历法，是行不通的，不应该一个一个出队列* 而是两个两个出队列*/
public class Case101 {public boolean isSymmetric1(TreeNode root) {Deque<TreeNode> queue = new LinkedList<>();queue.offerFirst(root.left);queue.offerLast(root.right);while (!queue.isEmpty()){TreeNode a = queue.pollFirst();TreeNode b = queue.pollLast();if (a == null && b == null){continue;}if (a == null && b != null)return false;if (a != null && b == null)return false;if (a.val != b.val)return false;queue.offerFirst(a.left);queue.offerFirst(a.right);queue.offerLast(b.right);queue.offerLast(b.left);}return true;}//递归法public boolean isSymmetric(TreeNode root) {return compare(root.left,root.right);}private boolean compare(TreeNode left, TreeNode right) {if (left == null && right != null)return false;if (left != null && right == null) return false;if (left == null && right == null)return true;if (left.val != right.val) return false;//比较外侧boolean compareOutside = compare(left.left,right.right);//比较内测boolean compareInside = compare(left.right,right.left);return compareInside && compareOutside;}
}

6、平衡二叉树

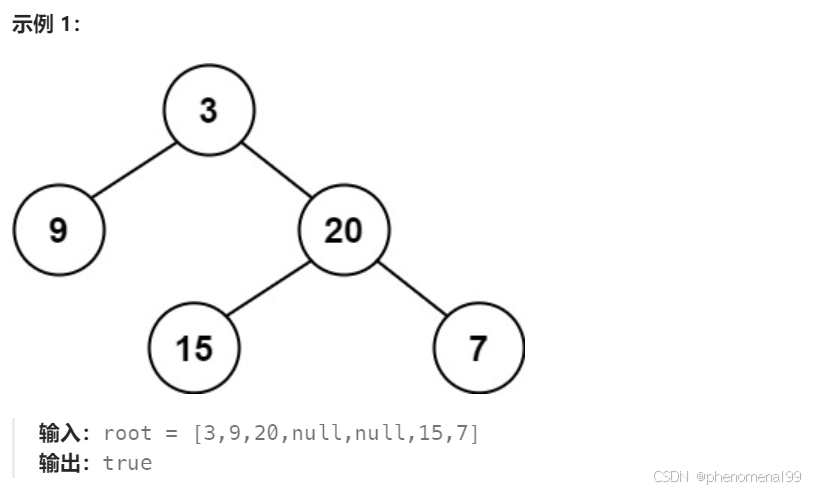
给定一个二叉树，判断它是否是高度平衡的二叉树。一棵高度平衡二叉树定义为：一个二叉树每个节点的左右两个子树的高度差的绝对值不超过1。

public class Case110 {public boolean isBalanced1(TreeNode root) {if (root == null) {return true;}int res = getHeight1(root);return res == -1 ? false : true;}private int getHeight1(TreeNode root) {if (root == null) return 0;int m = getHeight1(root.left);if (m == -1) return -1;int n = getHeight1(root.right);if (n == -1) return -1;if (Math.abs(m - n) > 1) return -1;return Math.max(m, n) + 1;}

7、二叉树的所有路径

给定一个二叉树，返回所有从根节点到叶子节点的路径。说明: 叶子节点是指没有子节点的节点。

这道题目要求从根节点到叶子的路径，所以需要前序遍历，这样才方便让父节点指向孩子节点，找到对应的路径。在这道题目中将第一次涉及到回溯，因为我们要把路径记录下来，需要回溯来回退一个路径再进入另一个路径。

前序遍历以及回溯的过程如图：

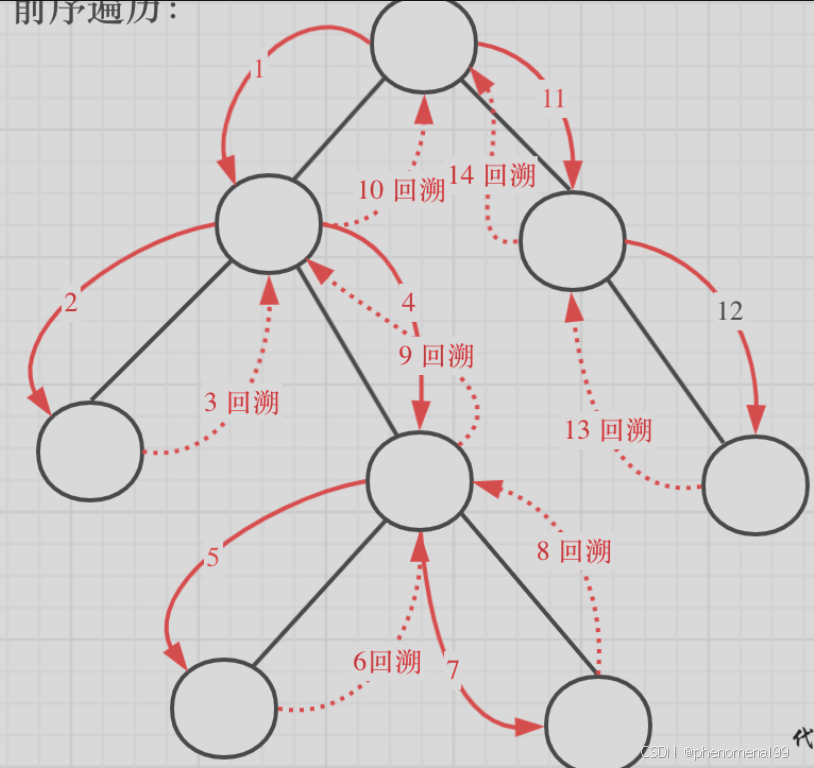
public class Case257 {public List<String> binaryTreePaths(TreeNode root) {List<String> res = new ArrayList<>();if (root == null){return res;}List<Integer> paths = new ArrayList<>(); //作为结果中的路径traversal(root,paths,res);return res;}//前序遍历private void traversal(TreeNode root, List<Integer> paths, List<String> res) {paths.add(root.val);//遇到叶子节点if(root.left == null && root.right == null){StringBuilder sb = new StringBuilder();for (int i = 0; i < paths.size()-1; i++) {sb.append(paths.get(i)).append("->");}sb.append(paths.get(paths.size() -1)); //记录最后一个节点res.add(sb.toString()); //收集一个路径return;}// 递归和回溯是同时进行，所以要放在同一个花括号里if (root.left != null){traversal(root.left,paths,res);paths.remove(paths.size() - 1); //回溯}if (root.right != null){traversal(root.right,paths,res);paths.remove(paths.size() - 1); //回溯}}//迭代法public List<String> binaryTreePaths1(TreeNode root) {List<String> result = new ArrayList<>();if (root == null)return result;//因为要掉头，所以不用队列要用栈了Stack<Object> stack = new Stack<>();//节点和路径同时ru栈stack.push(root);stack.push(root.val + "");while (!stack.isEmpty()){String path = (String) stack.pop();TreeNode node = (TreeNode) stack.pop();//若找到叶子节点if (node.left == null && node.right == null){result.add(path);}//右子节点不为空if (node.right != null){stack.push(node.right);stack.push(path + "->" + node.right.val);}//左节点不为空if (node.left != null){stack.push(node.left);stack.push(path + "->" + node.left.val);}}return result;}
}

8、左叶子之和

思路：层序遍历，该层的第一个元素且是叶子节点。

public class Case404 {// 递归(后续遍历)//如何只让左叶子节点加和？？？？？public int sumOfLeftLeaves(TreeNode root) {if (root == null)return 0;int a = sumOfLeftLeaves(root.left);int b = sumOfLeftLeaves(root.right);int midvaule = 0;if (root.left != null && root.left.left == null && root.left.right == null){midvaule = root.left.val;}int sum = midvaule + a + b;return sum;}//层序遍历public int sumOfLeftLeaves1(TreeNode root) {int sum = 0;if (root == null) return 0;Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);while (queue.isEmpty()){int len = queue.size();while (len-- > 0) {TreeNode node = queue.poll();if (node.left != null) {if (node.left.left == null && node.left.right == null) {sum += node.left.val;}}if (node.right != null) queue.offer(node.right);}}return  sum;}}

9、找树左下角的值

给定一个二叉树，在树的最后一行找到最左边的值。

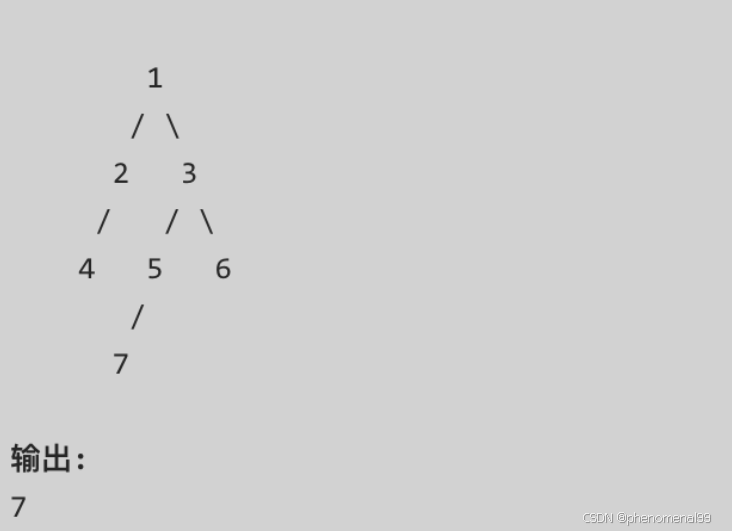
思路：层序遍历，至最后一行，拿到第一个元素

public class Case513 {private int DEEP = -1;private int value = 0;public int findBottomLeftValue(TreeNode root) {Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);int res = 0;while (!queue.isEmpty()){int len = queue.size();//这样写会导致res的值最后会变成最后一个出队列元素的值，所以这样写循环是不对的/*while (len-- > 0){TreeNode p = queue.poll();res = p.val;if (p.left != null)queue.offer(p.left);if (p.right != null)queue.offer(p.right);}}*/for (int i = 0; i < len; i++) {TreeNode p = queue.poll();if (i == 0) res = p.val;if (p.left != null)queue.offer(p.left);if (p.right != null)queue.offer(p.right);}}return res;}/*** 递归做法:* 1.确定最大深度，找到最后一层 维护一个全局变量DEEP* 2.因为是先对左孩子进行递归处理，也即先访问的左孩子。* 3.维护一个全局变量vaule来记录结果*/public int findBottomLeftValue1(TreeNode root) {value = root.val;findLeftVaule(root,0);return value;}private void findLeftVaule(TreeNode root, int deep) {if (root == null)return;if (root.left == null && root.right == null){if (deep > DEEP){value = root.val;DEEP = deep;}}if (root.left != null)findLeftVaule(root.left,deep + 1);if (root.right != null)findLeftVaule(root.right,deep + 1);}
}

10、路径总和

给定一个二叉树和一个目标和，判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和。说明: 叶子节点是指没有子节点的节点。示例: 给定如下二叉树，以及目标和 sum = 22

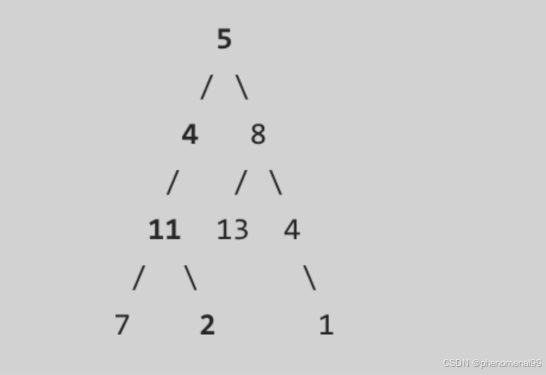
返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2。

public class Case112 {public boolean hasPathSum(TreeNode root, int targetSum) {if (root == null) return false;Stack<Object> stack = new Stack<>();stack.push(root);stack.push(root.val);while (!stack.isEmpty()){int res = (int) stack.pop();TreeNode node = (TreeNode) stack.pop();if (node.left == null && node.right == null){if (res == targetSum)return true;}if (node.right !=null){stack.push(node.right);stack.push(res + node.right.val);}if (node.left !=null){stack.push(node.left);stack.push(res + node.left.val);}}return false;}
}

11、构造二叉树

11.1 从中序与后序遍历序列构造二叉树

注意: 你可以假设树中没有重复的元素。

例如，给出

中序遍历 inorder = [9,3,15,20,7]
后序遍历 postorder = [9,15,7,20,3] 返回如下的二叉树：

public class Case106 {private static Map<Integer,Integer> map;public static void main(String[] args) {int[] inorder = {9,3,15,20,7};int[] postorder = {9,15,7,20,3};buildTree(inorder,postorder);}public static TreeNode buildTree(int[] inorder, int[] postorder) {map = new HashMap<>();for (int i = 0; i < inorder.length; i++) {map.put(inorder[i],i);}return findNode(inorder,0,inorder.length,postorder,0,postorder.length);}private static TreeNode findNode(int[] inorder, int inBegin, int inEnd, int[] postorder, int postBegin, int postEnd) {if (inBegin >= inEnd || postBegin >= postEnd){ //没有元素，返回空树,左闭右开[)return null;}int rootIndex = map.get(postorder[postEnd - 1]); //找到后续遍历的最后一个元素在中序遍历中的位置TreeNode root = new TreeNode(inorder[rootIndex]); //构造节点int lenOfLeft = rootIndex - inBegin; //保存中序左子树个数，用来确定后序数列的个数root.left = findNode(inorder,inBegin,rootIndex,postorder,postBegin,postBegin + lenOfLeft);root.right = findNode(inorder,rootIndex + 1,inEnd,postorder,postBegin+lenOfLeft,postEnd - 1);return root;}
}

11.2 从前序与中序遍历序列构造二叉树

public class Case105 {Map<Integer,Integer> map = new HashMap<>();public TreeNode buildTree(int[] preorder, int[] inorder) {for (int i = 0; i < inorder.length; i++) {map.put(inorder[i],i);}return findNode(inorder,0,inorder.length,preorder,0,preorder.length);}private TreeNode findNode(int[] inorder, int inBegin, int inEnd, int[] preorder, int preBegin, int preEnd) {if (inBegin >= inEnd || preBegin >= preEnd)return null;int rootIndex = map.get(preorder[preBegin]); //根节点在中序遍历中的索引TreeNode root = new TreeNode(inorder[rootIndex]);int lenOfLeft = rootIndex - inBegin;root.left = findNode(inorder,inBegin,rootIndex,preorder,preBegin + 1,preBegin + lenOfLeft + 1);root.right = findNode(inorder,rootIndex + 1,inEnd,preorder,preBegin+lenOfLeft + 1,preEnd);return root;}
}

11.3、最大二叉树

给定一个不含重复元素的整数数组。一个以此数组构建的最大二叉树定义如下：

二叉树的根是数组中的最大元素。
左子树是通过数组中最大值左边部分构造出的最大二叉树。
右子树是通过数组中最大值右边部分构造出的最大二叉树。

通过给定的数组构建最大二叉树，并且输出这个树的根节点。

/*** 给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:* 创建一个根节点，其值为 nums 中的最大值。* 递归地在最大值左边的子数组前缀上 构建左子树。* 递归地在最大值右边的子数组后缀上 构建右子树。* 返回 nums 构建的 最大二叉树*/
public class Case654 {public TreeNode constructMaximumBinaryTree(int[] nums) {if (nums == null)return null;return findNode(nums,0,nums.length);}private TreeNode findNode(int[] nums, int leftIndex, int rightIndex) {if (leftIndex >= rightIndex){  //数组不合法（左闭右开）return null;}int rootIndex = leftIndex;int max = nums[rootIndex];//max = Arrays.stream(nums).max().getAsInt(); //问题出在这，不应该在整个数组中找最大值了for (int i = leftIndex; i < rightIndex; i++) {if (nums[i] > max){max = nums[i];rootIndex = i;}}TreeNode root = new TreeNode(max);root.left = findNode(nums,leftIndex,rootIndex);root.right = findNode(nums,rootIndex + 1,rightIndex);return root;}
}

12、合并二叉树

给定两个二叉树，想象当你将它们中的一个覆盖到另一个上时，两个二叉树的一些节点便会重叠。你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠，那么将他们的值相加作为节点合并后的新值，否则不为 NULL 的节点将直接作为新二叉树的节点。

public class Case617 {public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {/*if (root1 == null) return root2;if (root2 == null) return root1;*/if (root1 == null || root2 == null) {return root1 == null ? root2:root1;}root1.val += root2.val;root1.left = mergeTrees(root1.left,root2.left);root1.right = mergeTrees(root1.right,root2.right);return root1;}
}

13、二叉搜索树

13.1 二叉搜索树中的搜索

给定二叉搜索树（BST）的根节点和一个值。你需要在BST中找到节点值等于给定值的节点。返回以该节点为根的子树。如果节点不存在，则返回 NULL。

 public TreeNode searchBST(TreeNode root, int val) {/* if (root == null) return null;if (root.val == val) return root;TreeNode left = searchBST(root.left,val);if (left != null){return left;}return searchBST(root.right,val);*///利用二叉搜索树的特点if (root == null || root.val == val) return root;if (root.val < val){return searchBST(root.right,val);}else {return searchBST(root.left,val);}}

13.2、验证二叉搜索树

给定一个二叉树，判断其是否是一个有效的二叉搜索树。假设一个二叉搜索树具有如下特征：

节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

/*** 验证二叉搜索树* 问题所在：不能局部判断，要保证左子树的全部节点都要比root小.......*/
public class Case98 {public boolean isValidBST(TreeNode root) {if (root == null) return true;/* if (root.left.val >= root.val || root.right.val <= root.val){return false;报空指针异常：如果左子树上来为空，那么问题就出现了}*/Boolean left = isValidBST(root.left);Boolean right = isValidBST(root.right);return  left && right;}//上述代码问题就出现在全局问题！！！public boolean isValidBST1(TreeNode root ){return isValidBSTHelper(root,Long.MIN_VALUE,Long.MAX_VALUE);}private boolean isValidBSTHelper(TreeNode root, long minValue, long maxValue) {if (root == null) return true;if (root.val <= minValue || root.val >= maxValue){return false;}//确定范围：左孩子一定要比根节点的值小，右孩子一定要比根节点的值要大return isValidBSTHelper(root.left,minValue, root.val) &&isValidBSTHelper(root.right, root.val, maxValue);}//迭代法public boolean isValidBST2(TreeNode root ){if (root == null) return true;Stack<TreeNode> stack = new Stack<>();TreeNode pre = null; //记录父节点while (root != null || !stack.isEmpty()){while (root != null){stack.push(root);root = root.left;}TreeNode pop = stack.pop();if (pre!=null && pop.val <= pre.val){return false;}pre = pop;root = root.right;}return true;}
}

13.3、二叉搜索树的最小绝对差

给你一棵所有节点为非负值的二叉搜索树，请你计算树中任意两节点的差的绝对值的最小值。

public class Case530 {int res = Integer.MAX_VALUE;TreeNode pre;  //记录上一个遍历的节点public int getMinimumDifference(TreeNode root) {func(root);return res;}private void func(TreeNode root) {if (root == null) return;func(root.left);if (pre != null) {res = Math.min(res, root.val - pre.val);}pre = root;func(root.right);}//迭代法-中序遍历public int getMinimumDifference1(TreeNode root) {if (root == null) return 0;TreeNode pre = null;Stack<TreeNode> stack = new Stack<>();TreeNode cur = root;int res = Integer.MAX_VALUE;while (cur != null || !stack.isEmpty()) {if (cur != null) {stack.push(cur); //将要访问的节点放进栈cur = cur.left;} else {cur = stack.pop();if (pre != null) { //中res = Math.min(res, cur.val - pre.val);}pre = cur;cur = cur.right; //右}}return res;}
}

13.4 二叉搜索树中的众数

给定一个有相同值的二叉搜索树（BST），找出 BST 中的所有众数（出现频率最高的元素）。结果集合中可以是多个元素。

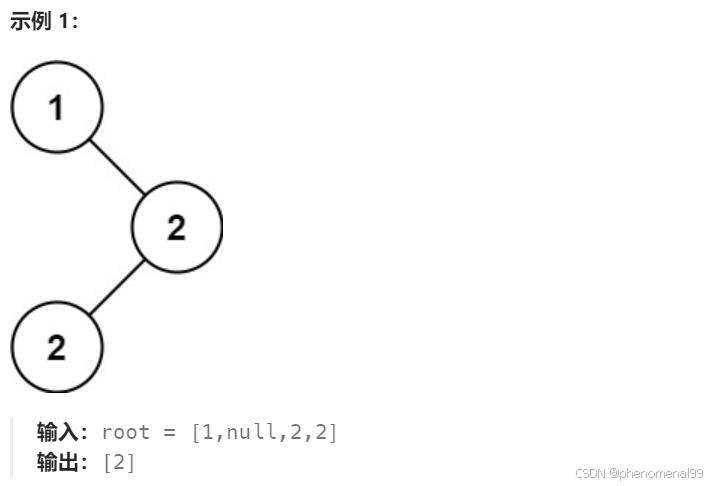
思路：定义全局变量 count 记录节点值出现的次数，maxCount记录出现次数最多的节点值，

public class Case501 {//迭代遍历public int[] findMode(TreeNode root) {if(root == null)return null;List<Integer> res = new ArrayList<>();int maxCount = 0;int count = 0;TreeNode pre = null;Stack<TreeNode> stack = new Stack<>();TreeNode cur = root;while (cur != null || !stack.isEmpty()){if (cur != null){stack.push(cur);cur = cur.left;}else {cur = stack.pop();if (pre == null || pre.val != cur.val){count = 1;}else {count ++;}//更新结果if (count > maxCount){maxCount = count;res.clear();   //重新清空集合res.add(cur.val);}else if (count == maxCount){res.add(cur.val);}pre = cur;cur = cur.right;}}int[] a = new int[res.size()];for (int i = 0; i < res.size(); i++) {a[i] = res.get(i);}return a;//return res.stream().mapToInt(Integer:: intValue).toArray();}
}

13.5 二叉树的最近公共祖先

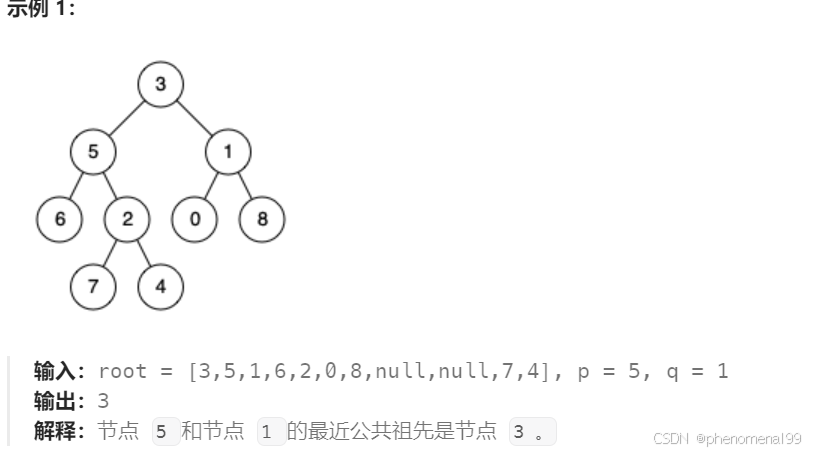
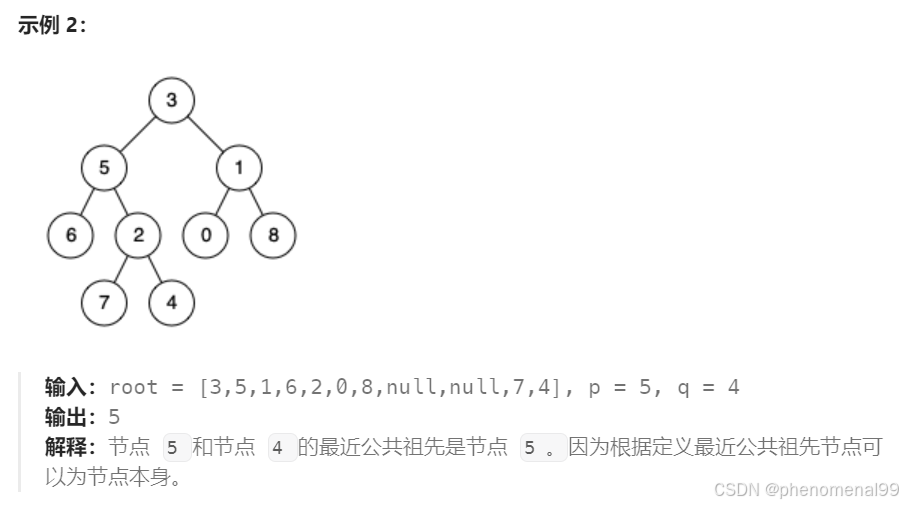
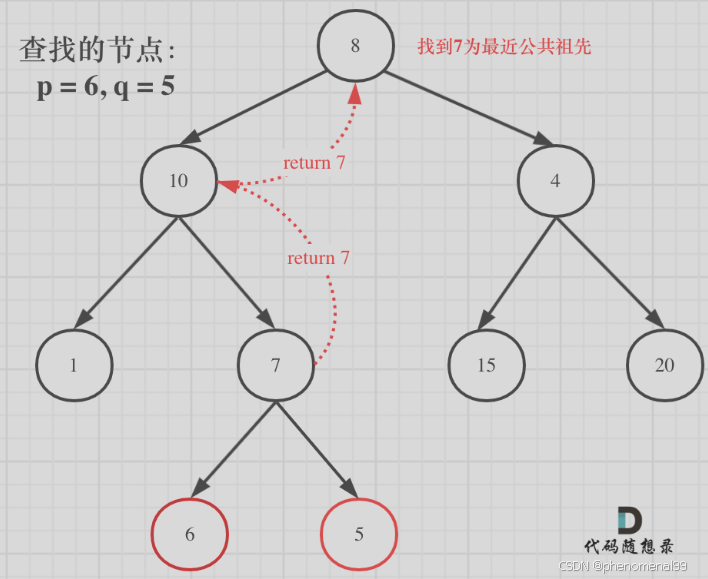
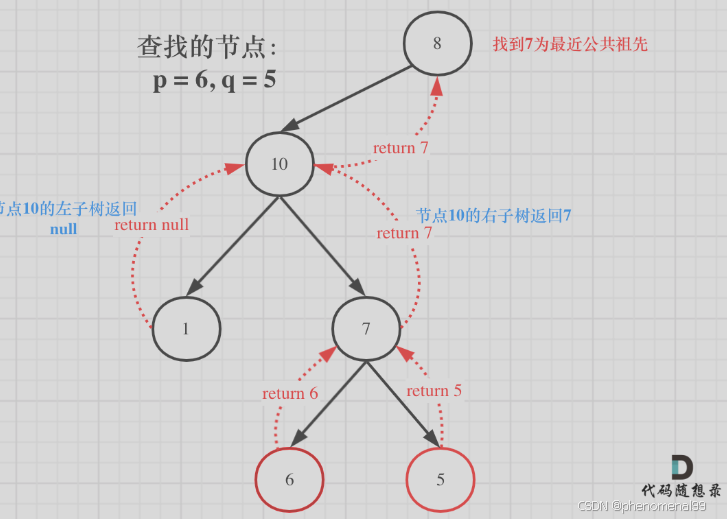
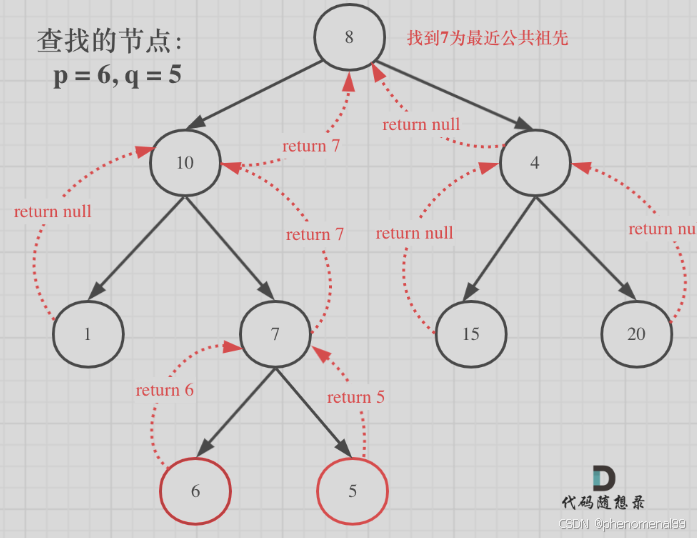
public class Case236 {/*** 1.求最小公共祖先，需要从底向上遍历，二叉树，只能通过后序遍历，实现从底向上的遍历方式* 2.在回溯过程中，必然要遍历整颗二叉树，即使已经找到结果了，依然要把其他节点遍历完，因为要使用递归函数的* 返回值* 3.要理解如果返回值为空，right不为空为什么要返回right，为什么可以用返回right传给上一层结果。* 可以说这里每一步，都是有难度的，都需要对二叉树，递归和回溯有一定的理解。*本题没有给出迭代法，因为迭代法不适合模拟回溯的过程。理解递归的解法就够了。*///写得太牛逼了!!!! 值得反复揣摩。优雅public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {if (root == null || root == p || root == q){ //强啊return root;}//后序遍历TreeNode left = lowestCommonAncestor(root.left,p,q);TreeNode right = lowestCommonAncestor(root.right,p,q);if (left == null && right == null){ //如果未找到节点p或qreturn null;}else if (left == null && right != null){ //若找到一个节点return right;}else if (left != null && right == null){return left;}else { // 若找到两个节点return root;}}
}

13.6 二叉搜索树的最近公共祖先

public class Case235 {public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {if(root == null) return null;
// 如果一个节点比root大，一个比root小，那就最近祖先就是root了啊while (root != null){if (root.val > p.val && root.val > q.val){root = root.left;}else if (root.val < p.val && root.val < q.val){root = root.right;}else {break;}}return root;}//递归public TreeNode lowestCommonAncestor1(TreeNode root, TreeNode p, TreeNode q) {if (root.val > p.val && root.val > q.val){return lowestCommonAncestor(root.left,p,q);}if (root.val < p.val && root.val < q.val){return lowestCommonAncestor(root.right,p,q);}return root;}
}

13.7 二叉搜索树中的插入操作

给定二叉搜索树（BST）的根节点和要插入树中的值，将值插入二叉搜索树。返回插入后二叉搜索树的根节点。输入数据保证，新值和原始二叉搜索树中的任意节点值都不同。注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。你可以返回任意有效的结果。

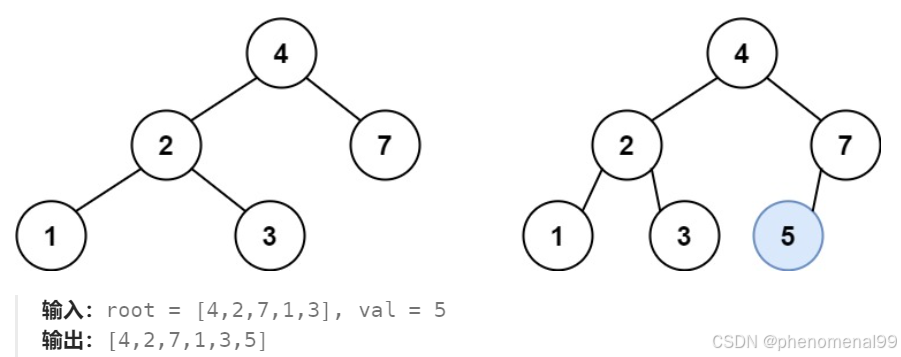
public class Case701 {public TreeNode insertIntoBST(TreeNode root, int val) {if (root == null){TreeNode p = new TreeNode(val);return p;}if (root.val > val){root.left = insertIntoBST(root.left,val);}else {root.right = insertIntoBST(root.right,val);}return root;}//非递归public TreeNode insertIntoBST1(TreeNode root, int val) {if (root == null) return new TreeNode(val);TreeNode newRoot = root;TreeNode pre = root;while (root != null){pre = root;if (root.val > val){root = root.left;}else if (root.val < val){root = root.right;}}if (pre.val > val){pre.left = new TreeNode(val);}else {pre.right = new TreeNode(val);}return newRoot;}
}

13.8 删除二叉搜索树中的节点

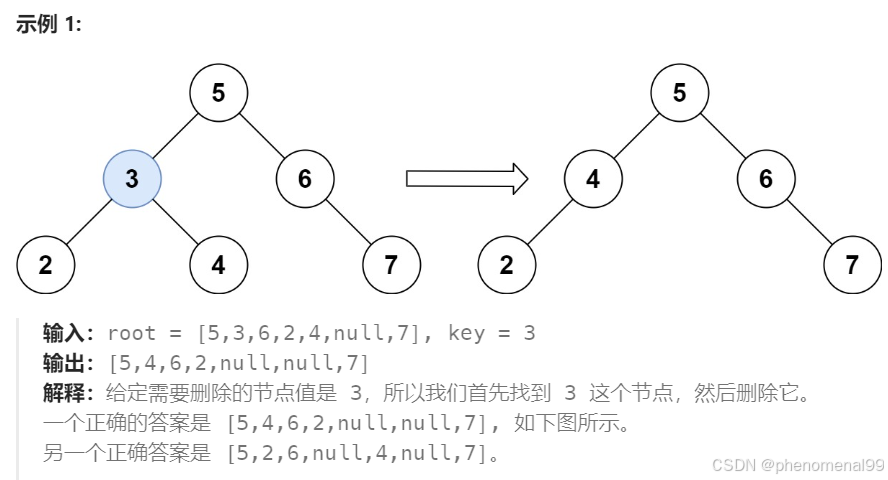
class Solution {public TreeNode deleteNode(TreeNode root, int key) {if (root == null) return root;if (root.val == key) {if (root.left == null) {return root.right;} else if (root.right == null) {return root.left;} else {TreeNode cur = root.right;while (cur.left != null) {cur = cur.left;}cur.left = root.left;root = root.right;return root;}}if (root.val > key) root.left = deleteNode(root.left, key);if (root.val < key) root.right = deleteNode(root.right, key);return root;}
}

13.9 修剪二叉搜索树

给定一个二叉搜索树，同时给定最小边界L 和最大边界 R。通过修剪二叉搜索树，使得所有节点的值在[L, R]中 (R>=L) 。你可能需要改变树的根节点，所以结果应当返回修剪好的二叉搜索树的新的根节点。

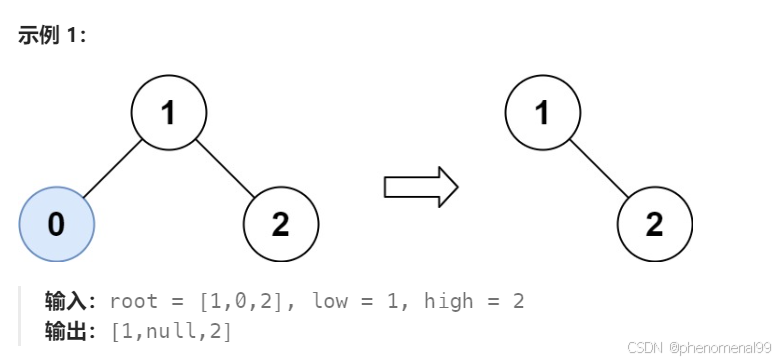
public class Case669 {public TreeNode trimBST(TreeNode root, int low, int high) {if(root == null || low > high) return root;//如果根节点就不在合法范围内，那就先找到第一个合法的节点while (root != null && (root.val < low || root.val > high)){if (root.val < low){root = root.right;}else {root = root.left;}}TreeNode curr = root;//处理左子树while (curr != null){while (curr.left != null && curr.left.val < low){curr.left = curr.left.right;}curr = curr.left;}curr = root;  //重新回到根节点//处理右子树while (curr != null){while (curr.right != null && curr.right.val > high){curr.right = curr.right.left;}curr = curr.right;}return root;}//递归public TreeNode trimBST1(TreeNode root, int low, int high) {/*if (root == null || root.val < low || root.val > high) return null;root.left = trimBST(root.left, low, high);root.right = trimBST(root.right, low, high);return root;*/if (root == null){return null;}if (root.val < low){return trimBST1(root.right,low,high);}if (root.val > high){TreeNode a = trimBST1(root.left,low,high);return a;}//root 在合法的范围内root.left = trimBST1(root.left,low,high);root.right = trimBST1(root.right,low,high);return root;}
}

13.10 将有序数组转换为二叉搜索树

将一个按照升序排列的有序数组，转换为一棵高度平衡二叉搜索树。本题中，一个高度平衡二叉树是指一个二叉树每个节点的左右两个子树的高度差的绝对值不超过 1。

public TreeNode sortedArrayToBST(int[] nums) {if (nums == null) return null;return sortedArrayToBST(nums,0,nums.length);}private TreeNode sortedArrayToBST(int[] nums, int left, int right) {if (left >= right){  //要求左闭右开return null;}int mid = (left + right) / 2;TreeNode root = new TreeNode(nums[mid]);root.left = sortedArrayToBST(nums,left,mid);root.right = sortedArrayToBST(nums,mid + 1,right);return root;}
}

13.11 把二叉搜索树转换为累加树

给出二叉搜索树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。提醒一下，二叉搜索树满足下列约束条件：节点的左子树仅包含键小于节点键的节点。节点的右子树仅包含键大于节点键的节点。左右子树也必须是二叉搜索树。

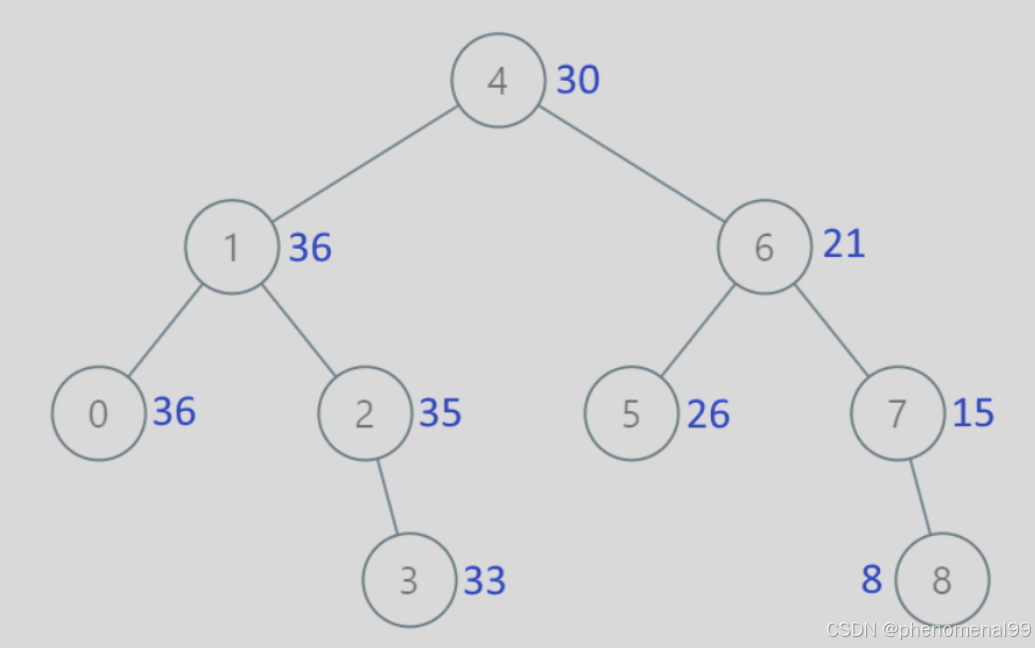
public class Case538 {private  int num = 0;public TreeNode convertBST(TreeNode root) {if (root == null)return null;/*root.right = convertBST(root.right);if (root.right != null){root.val = root.val + root.right.val;}root.left = convertBST(root.left);if (root.left != null){root.left.val = root.val + root.left.val;}return root;*///上述代码虽然遵从了逆中序遍历，但是由于递归，convertBST(root.right);root.val = root.val + num;num = root.val;convertBST(root.left);return root;}
}