基本概念



-
满二叉树
-
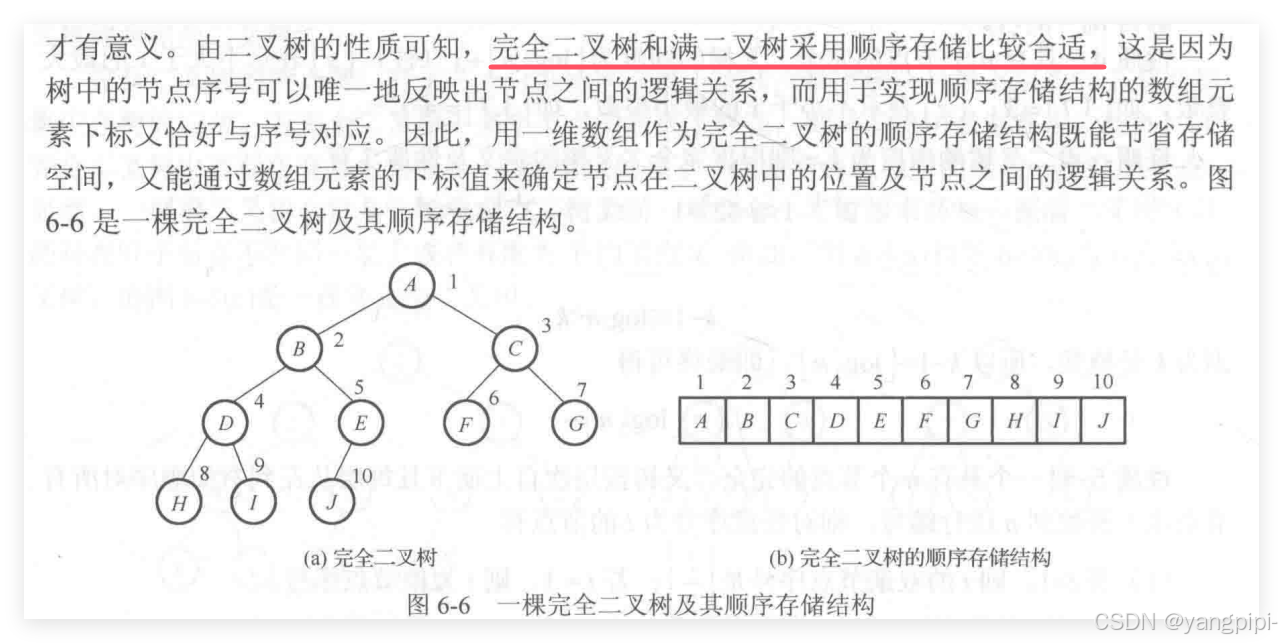
完全二叉树
-

二叉树的性质





二叉树的存储结构
顺序存储结构
链式存储结构

二叉树的遍历(以二叉链表为例)
前序遍历
递归遍历
void Preorder(BSTree* p)
{if (p != NULL){printf("%c ",p->data);Preorder(p->lchild);Preorder(p->rchild);}
}
非递归遍历


void PreorderNoRecursive(BSTree* p)
{/*思路: 不断遍历左子树然后将其入栈,知道遇到NULL,弹栈,然后指向弹出元素的右子树*/std::stack<BSTree*> sta;while (p!=NULL || !sta.empty()){if (p!=NULL){printf("%c ", p->data);sta.push(p);p = p->lchild;}else{p = sta.top();sta.pop();p = p->rchild;}}
}
中序遍历
递归遍历
void Inorder(BSTree* p)
{if (p != NULL){Inorder(p->lchild);printf("%c ", p->data);Inorder(p->rchild);}
}
非递归遍历

void InorderNoRecursive(BSTree* p)
{/*思路: 不断将左子树入栈,直到遇到NULL,弹栈,访问,然后指向弹出元素的右子树*/std::stack<BSTree*> sta;while (p != NULL || !sta.empty()){if (p != NULL){sta.push(p);p = p->lchild;}else{p = sta.top();sta.pop();printf("%c ", p->data);p = p->rchild;}}
}
后序遍历
递归遍历
void Postorder(BSTree* p)
{if (p != NULL){Postorder(p->lchild);Postorder(p->rchild);printf("%c ", p->data);}
}
非递归遍历(困难)

设置访问标志b(一层)



void PostorderNoRecursive1(BSTree* p)
{BSTree* sta[MAXSIZEBS];int i = 0, b[MAXSIZEBS];sta[0] = NULL;do{if (p != NULL){sta[++i] = p;b[i] = 0; // 置*p的右子树未访问过的标志p = p->lchild;}else{p = sta[i--];if (b[i + 1] == 0){sta[++i] = p;b[i] = 1; // 置*p的右子树已访问的标志p = p->rchild;}else{printf("%c ",p->data);p = NULL; // 指向*p的指针置空}}} while (p != NULL || i > 0);
}
二层循环


前序-> 后序

先依次将右子树依此压栈,直到右子树为NULL时,再压栈,访问此元素的左子树。最后将得到的元素反向输出即可。
void PostorderNoRecursive(BSTree* p)
{std::stack<BSTree*> sta;std::vector<char> vec;while (p != NULL || !sta.empty()){if (p != NULL){//printf("%c ", p->data);vec.push_back(p->data);sta.push(p);p = p->rchild;}else{p = sta.top();sta.pop();p = p->lchild;}}for (std::vector<char>::const_reverse_iterator it = vec.rbegin(); it != vec.rend(); it++){printf("%c ",*it);}
}
层次遍历
void Transleve(BSTree* t)
{/*使用队列,依次访问每一个元素。*/// 层次遍历的方式一//std::queue<BSTree*> de;//BSTree* p;//if (t != NULL)//{// printf("%c ", t->data);// de.push(t);//}//else // return;//while (!de.empty())//{// p = de.front();// de.pop();// if (p->lchild != NULL)// {// printf("%c ", p->lchild->data);// de.push(p->lchild);// }// if (p->rchild != NULL) //注意这里不是else if// {// printf("%c ", p->rchild->data);// de.push(p->rchild);// }//}// 层次遍历的方式2:std::queue<BSTree*> de;BSTree* p;if (t != NULL)de.push(t);else return;while (!de.empty()){p = de.front();printf("%c ", p->data);de.pop();if (p->lchild != NULL)de.push(p->lchild);if (p->rchild != NULL)de.push(p->rchild);}}
练习题
根据条件交换二叉树的左右子树

void Change(BSTree* p)
{if (p != NULL){if (p->lchild!=NULL&& p->rchild!=NULL&&p->lchild->data > p->rchild->data) // 如果左子树大于右子树的话,就交换左右子树{BSTree* tmp = p->lchild;p->lchild = p->rchild;p->rchild = tmp;}Change(p->lchild);Change(p->rchild);}
}
查找元素
根据中序非递归查找
// 查找
// 搜素 根据中序非递归遍历查找元素
BSTree* Search_In_NoRecursive(BSTree* p, datatypeBS x)
{std::stack<BSTree*> sta;while (p != NULL || !sta.empty()){if (p != NULL){sta.push(p);p = p->lchild;}else{p = sta.top();sta.pop();//printf("%c ", p->data);if (p->data == x)return p;p = p->rchild;}}return NULL;
}
根据先序递归查找(易错)

BSTree* Search_Pre_Recursive(BSTree* bt, datatypeBS x)
{BSTree* p = NULL;if (bt != NULL){/*printf("%c ", p->data);*/if (bt->data == x)return bt;if (bt->lchild != NULL){p = Search_Pre_Recursive(bt->lchild, x);if (p != NULL)return p;}if (bt->rchild != NULL){p = Search_Pre_Recursive(bt->rchild, x);if (p != NULL)return p;}}return NULL;
}

统计二叉树中叶子节点的个数
递归方法
// 统计叶子节点的个数
int Countleaf(BSTree* p)
{if (p == NULL) // 空二叉树return 0;if (p->lchild == NULL && p->rchild == NULL) // 叶子节点return 1;return Countleaf(p->lchild) + Countleaf(p->rchild);
}
非递归方法

int Countleaf_PreorderNoRecursive(BSTree* p)
{/*思路: 不断遍历左子树然后将其入栈,知道遇到NULL,弹栈,然后指向弹出元素的右子树*/int count = 0;std::stack<BSTree*> sta;while (p != NULL || !sta.empty()){if (p != NULL){//printf("%c ", p->data);if (p->lchild == NULL && p->rchild == NULL)count++;sta.push(p);p = p->lchild;}else{p = sta.top();sta.pop();p = p->rchild;}}return count;
}
求二叉树深度

// 求二叉树的深度
int Depth(BSTree* p)
{int lchild = 0, rchild = 0;if (p == NULL)return 0;else {lchild = Depth(p->lchild)+1;rchild = Depth(p->rchild)+1;return lchild > rchild ? lchild : rchild;}
}
判断二叉树是否是完全二叉树

- 利用层序遍历,在将一个节点压入队列之前,如果其有右孩子而没有左孩子时则不是满二叉树。
// 判断一个二叉树是否是完全二叉树
int is_complete_binary_tree(BSTree* t)
{std::queue<BSTree*> de;BSTree* p;if (t != NULL)de.push(t);elsereturn 1;while (!de.empty()){p = de.front();//printf("%c ", p->data);de.pop();if (p->lchild != NULL)de.push(p->lchild);else{if (p->rchild != NULL)return 0; // 不是完全二叉树}if (p->rchild != NULL)de.push(p->rchild);}return 1; // 是完全二叉树
}
找出二叉树中最深的通道

// 求二叉树的最长深度并输出数值
int len = 0;
int longest_len = 0;
void longest_path(BSTree* T, char* path, char* longestpath)
{int j, i;if (T)//树不空{if (!T->lchild && !T->rchild)//当遇到叶子结点时,该条路径完毕 {path[len] = T->data;//把结点数据放入数组 if (len > longest_len)//如果长于longest_len就替换 {for (j = 0; j <= len; j++)//把路径复制到longestpath里面 longestpath[j] = path[j];longest_len = len;//longest_len更新 }}else//当遇到的不是叶子结点时,该条路径继续 {path[len++] = T->data;//结点放入数组,len++ longest_path(T->lchild, path, longestpath);longest_path(T->rchild, path, longestpath);len--;//每次退出递归len-- }}
}
注意,定义全局遍历的不要再头文件中定义。应该在一个.c文件中定义并且初始化。如果其他.c文件想使用的话,需要在头文件中使用·extern声明注意注意只是声明不要初始化。
在a.c中 int num = 1; 在a.h中 extern int num; 在b.c中只需要#include"a.h"即可在b.c中使用定义的全局变量num
二叉树的创建
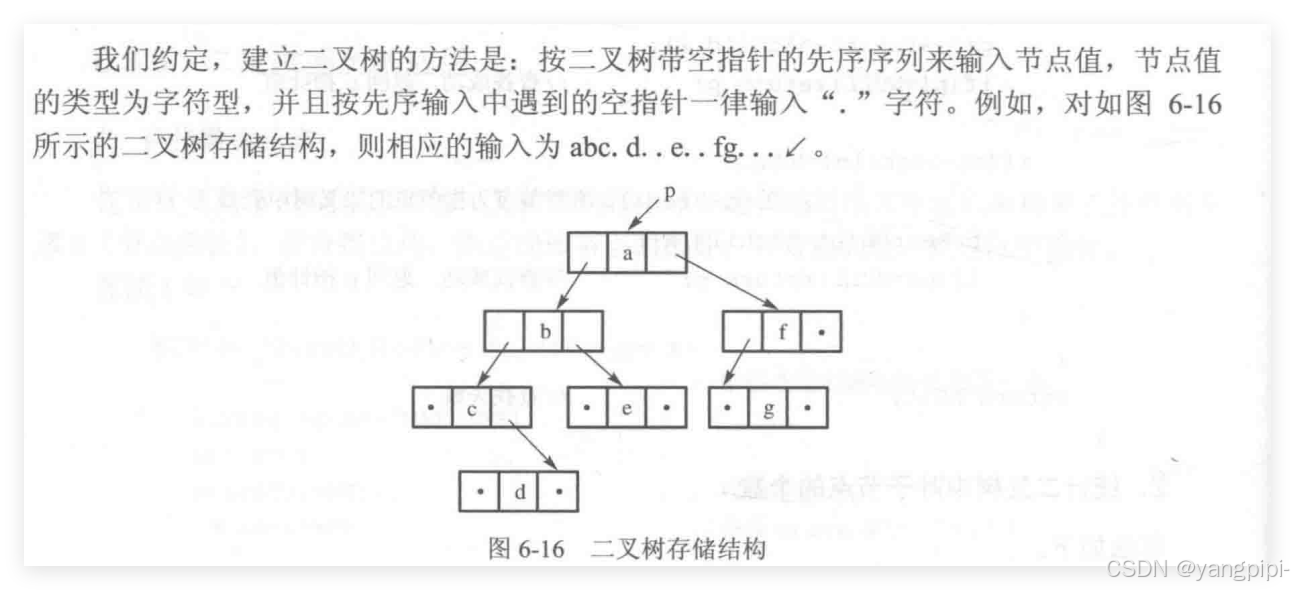
根据先序序列创建
void CreatebByPreorder(BSTree** p)
{char ch;scanf("%c",&ch);if (ch != '.'){*p = (BSTree*)malloc(sizeof(BSTree));(*p)->data = ch;CreatebByPreorder(&((*p)->lchild));CreatebByPreorder(&((*p)->rchild));}else*p = NULL;
}
由遍历序列恢复二叉树
-
先序+中序 -》 可恢复
-

-
后序+中序-》可恢复
-

先序+中序 -》二叉树

在这里插入图片描述
// 根据 先序+中序-》 二叉树
void Pre_In_Oreder(char pred[], char ind[], int i, int j, int k, int h, BSTree** p)
{*p = (BSTree*)malloc(sizeof(BSTree));(*p)->data = pred[i]; // 首先构造头结点// 从中序序列中找到头结点的位置int m = k;while (ind[m] != pred[i])m++;// 构造左子树if (m == k) // 左子树为NULL(*p)->lchild = NULL;elsePre_In_Oreder(pred,ind,i+1, i+m-k,k,m-1,&(*p)->lchild);// 构造右子树if (m == h) // 右子树为NULL(*p)->rchild = NULL;elsePre_In_Oreder(pred, ind, i + m - k+1, j , m+1, h, &(*p)->rchild);
}
- 主要是每次遍历先序序列的范围


int main()
{BSTree* tree1;char pred[] = "acbgdehfji";char ind[] = "cgbahedjfi";Pre_In_Oreder(pred, ind, 0, 9, 0, 9, &tree1); //void Pre_In_Oreder(char pred[], char ind[], int i, int j, int k, int h, BSTree** p)printf("\nTransleve遍历结果:");Transleve(tree1);printf("\nPostorder遍历结果:");Postorder(tree1);return 0;
}
后序+中序 -》二叉树

void Post_In_Oreder(char post[], char ind[], int i, int j, int k, int h, BSTree** p)
{*p = (BSTree*)malloc(sizeof(BSTree));(*p)->data = post[j]; // 首先构造头结点// 从后序序列中找到头结点的位置int m = k;while (ind[m] != post[j])m++;// 构造左子树if (m == k) // 左子树为NULL(*p)->lchild = NULL;elsePost_In_Oreder(post, ind, i, i + m - k-1, k, m - 1, &(*p)->lchild);// 构造右子树if (m == h) // 右子树为NULL(*p)->rchild = NULL;elsePost_In_Oreder(post, ind, i + m - k, j-1, m + 1, h, &(*p)->rchild);
}
线索二叉树



线索化二叉树



// 线索二叉树————————————————
// 中序线索二叉树
void Thread(TBTree* p) // 对二叉树的进行线索化
{if (p != NULL){Thread(p->lchild);if (p->lchild == NULL){p->ltag = 1;p->lchild = pre;}else {p->ltag = 0;}if (pre->rchild == NULL){pre->rtag = 1;pre->rchild = p;}else {pre->rtag = 0;}pre = p;Thread(p->rchild);}
}TBTree* CreatThread(TBTree* b)// 建立中序线索二叉树
{TBTree* root;root = (TBTree*)malloc(sizeof(TBTree));root->ltag = 0;root->rtag = 1;if (b == NULL)root->lchild = root;else {root->lchild = b;pre = root;Thread(b);pre->rchild = root;pre->rtag = 1;root->rchild = pre;}return root;
}
访问线索二叉树
1. 在中序线索二叉树上查找任意节点的中序前驱节点

//在中序线索二叉树上查找任意节点p的中序前驱节点
TBTree* Inpre(TBTree* p)
{TBTree* tmp;if (p->ltag == 1)return p->lchild;else { // 有右孩子 :p的前驱节点就是以p为根节点的子树的最右节点TBTree* tmp = p->lchild;while (tmp->rtag == 0) //rtag为0表示有孩子tmp = tmp->rchild;}
}
2. 在中序线索二叉树上查找任意节点的中序后继节点

//在中序线索二叉树上查找任意节点的中序后继节点
TBTree* InPoost(TBTree* p)
{TBTree* tmp;if (p->rtag == 1) // 没有左孩子return p->rchild;else { // 有右孩子:则p的后继节点就是以p的右孩子为子树的最左节点tmp = p->rchild;while (tmp->ltag == 0)tmp = tmp->lchild;}
}
3. 中序遍历中序线索二叉树

void Inorder(TBTree* b)
{TBTree* p = b->lchild;while (p != b){while (p->ltag == 0) // 找到第一个节点p = p->lchild;printf("%c ",p->data); while (p->rtag == 1 && p != b) // 当后继线索存在且不是头结点时{printf("%c ",p->data);p = p->rchild;}p = p->rchild;}
}
哈夫曼树(最优二叉树)


哈夫曼树构造




哈夫曼算法


树和森林
树的存储结构








树->二叉树
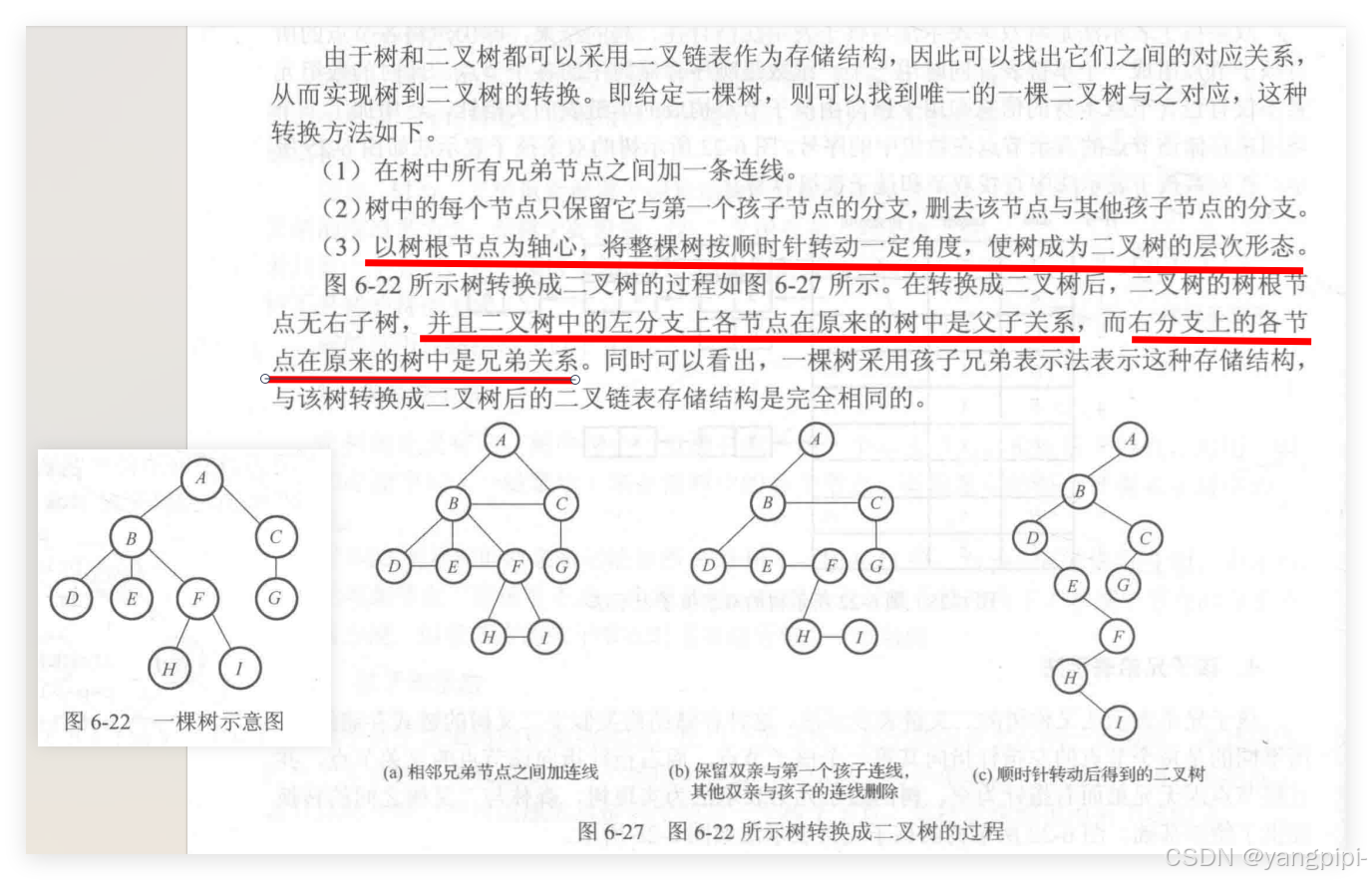
森林->二叉树
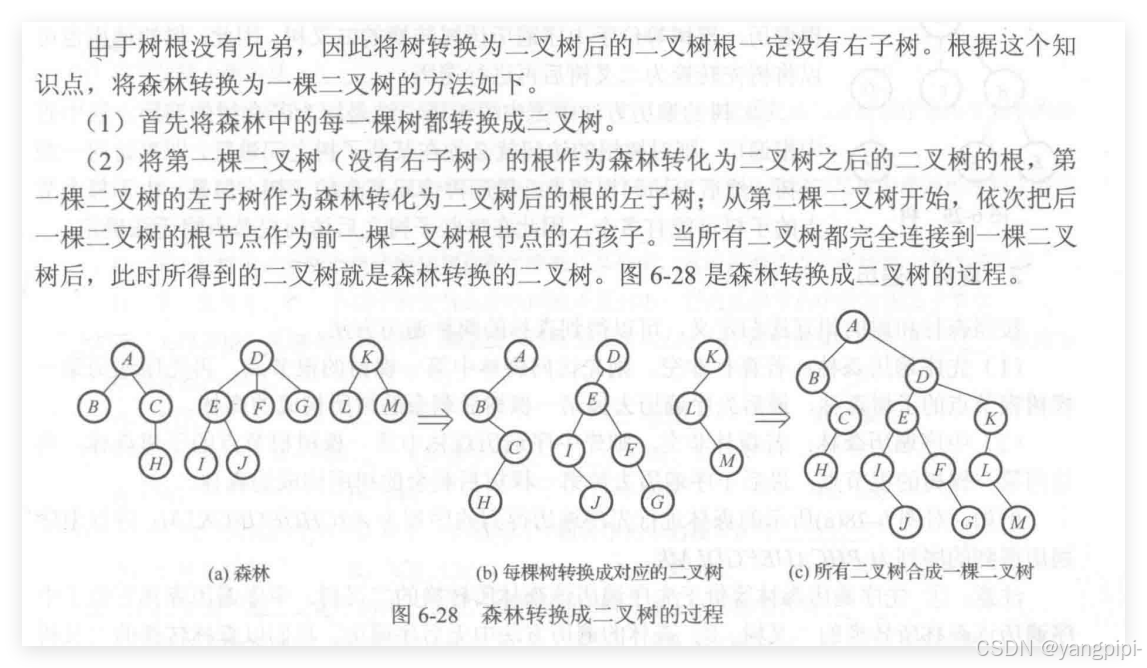
二叉树转换为树和森林

树的遍历



森林的遍历


