👂 ▶ 怀抱的温柔并不属于我(弹唱版) (163.com)
👂 ▶ Gotta Have You (163.com)
👂 ▶ 心许百年 (163.com)
目录
🚩岛屿数量
AC DFS
AC BFS
AC 并查集
解释
代码
🌼腐烂的橘子
AC 多源bfs
🎂课程表
前置知识
AC BFS
🌼实现 Trie(前缀树)
解释
坑
代码
🚩岛屿数量
200. 岛屿数量 - 力扣(LeetCode)
AC DFS
同 bfs,采用 flood fill 大水漫灌,也称感染法
if(grid[x][y] == '1') 对每个点进行 dfs,将走过的陆地 “1” 标记为 “0”
然后套模板
时间 O(mn):每个点遍历 1 次;空间 O(mn):所有点均为陆地,递归深度 m*n
class Solution {
public:int ans; int nex[4][2] = {{0,1},{1,0},{0,-1},{-1,0}}; // 4 个方向// 从 x, y 开始深度优先搜索void dfs(vector<vector<char>>& grid, int x, int y) {int m = grid.size(), n = grid[0].size();grid[x][y] = '0'; // 大水漫灌 / 感染法for (int i = 0; i < 4; ++i) { // 新的坐标int xx = x + nex[i][0], yy = y + nex[i][1];// 下一位置满足要求才递归,类似递归出口的处理if (xx < m && yy < n && xx >= 0 && yy >= 0 && (grid[xx][yy] == '1') )dfs(grid, xx, yy);}}int numIslands(vector<vector<char>>& grid) {int m = grid.size(), n = grid[0].size();for (int i = 0; i < m; ++i)for (int j = 0; j < n; ++j)if (grid[i][j] == '1') {ans++; // 岛屿数量 +1dfs(grid, i, j);}return ans;}
};AC BFS
同 dfs,采用 flood fill 大水漫灌,也称感染法
if(grid[x][y] == '1') 对每个点进行 bfs,将走过的陆地 “1” 标记为 “0”
然后套模板
注意 queue 的声明,queue<pair<int, int>>,而非 queue<int, int>,因为 queue, stack, vector 这种,只能放一个参数;两个参数的是 map<int, int> 和 unordered_map<int, int>
第 31 行,遍历 4 个方向那里,越界的话,是 continue 不是 break,常犯错误
时间 O(mn),空间 O(min(m, n))
class Solution {
public:int ans = 0; // 岛屿数量int nex[4][2] = {{0,1},{0,-1},{1,0},{-1,0}}; // 4 个方向int numIslands(vector<vector<char>>& grid) {queue<pair<int, int>> q; // 横纵坐标int m = grid.size(), n = grid[0].size();// 对陆地上每个点 bfsfor (int i = 0; i < m; ++i)for (int j = 0; j < n; ++j) if (grid[i][j] == '1') { // 只对陆地 bfsq.push({i, j}); // 入队ans++;grid[i][j] = '0'; // 大水漫灌 / 感染法// 逐层扩展while (!q.empty()) {auto cur = q.front(); // 取队头q.pop();int x = cur.first, y = cur.second; // 取坐标// 4 个方向扩展for (int k = 0; k < 4; ++k) {int xx = x + nex[k][0], yy = y + nex[k][1];if (xx < 0 || yy < 0 || xx >= m || yy >= n)continue; // 不是 breakif (grid[xx][yy] == '1') { q.push({xx, yy});grid[xx][yy] = '0'; // 感染法}}}}return ans;}
};AC 并查集
解释
1)dad[] 是父节点数组,这里用一维表示二维,每个坐标 x, y 在 dad 里表示为 x*n + y
表示 第 x 行,第 y 列
2)初始化 dad 为二维坐标的一维表示,比如,grid[3][4] == '1',假设 4 行 5 列,m=4, n=5
那么 dad[3*5 + 4] = 3*5 + 4,即 dad[19] == 19,自己是自己的祖先
3)初始化时,每次遇到 '1',count++
join() 合并两个陆地时,count--
最后 count 就是岛屿数量
比如,初始化时,count == 5,有 5 块陆地,全图遍历时,合并了 3 次,
5 - 3 = 2,岛屿数量为 2
4)每次 join() 合并完,dad[] 里的数就 = 祖先,比如 dad[0], dad[1], dad[2] 都是 0
表示第 0 行前 3 个数都是一块陆地的
5)join() 合并函数中,count--,要放在 if (xx != yy) {} 里,如果相等,说明不需要合并
6)dad 是 vector 的话,记得 resize() 大小
代码
class Solution {
public:int dad[90000];int count = 0; // 岛屿数量int nex[4][2] = {{1,0},{-1,0},{0,1},{0,-1}}; // 4 个方向// 找领头int Find(int x) { if (dad[x] == x)return x;elsereturn dad[x] = Find(dad[x]); // 路径压缩}// 合并两个团体void join(int x, int y) {int xx = Find(x), yy = Find(y);if (xx != yy) {dad[yy] = xx;count--; // 合并陆地后,岛屿数量 -1}}int numIslands(vector<vector<char>>& grid) {int m = grid.size(), n = grid[0].size();// dad.resize(m*n); // 声明大小// 初始化 dad[]for (int i = 0; i < m; ++i)for (int j = 0; j < n; ++j)if (grid[i][j] == '1') {count++;dad[n*i + j] = n*i + j; // 自己的祖先是自己}// 全图遍历for (int i = 0; i < m; ++i)for (int j = 0; j < n; ++j) if (grid[i][j] == '1') {grid[i][j] = '0'; // 防止多次合并同一块陆地// 对 4 个方向进行合并for (int k = 0; k < 4; ++k) {// 新的坐标int x = i + nex[k][0], y = j + nex[k][1];if (x < 0 || y < 0 || x >= m || y >= n)continue;if (grid[x][y] == '1')join(n*i + j, n*x + y); // 合并两点}}return count;}
};🌼腐烂的橘子
994. 腐烂的橘子 - 力扣(LeetCode)
AC 多源bfs
和单源 bfs 不同的是,每个腐烂橘子,往上下左右 4 个方向扩散,所以,在 while (!q.empty && fresh > 0)
下,要多加一个 for (int size = q.size(); size >= 0; --size)
多这个一个 for 表示,单源 bfs 从一个点开始往四周扩散,而多源 bfs,从当前所有腐烂的点同时开始扩散

时空 O(mn)
class Solution {
public:int orangesRotting(vector<vector<int>>& grid) {int nex[4][2] = {{1,0},{-1,0},{0,1},{0,-1}};queue<pair<int, int>> q; // 存放坐标的队列int fresh = 0; // 新鲜橘子数int m = grid.size(), n = grid[0].size();int min = 0;// 初始化:得到新鲜橘子数 && 腐烂橘子加入队列for (int i = 0; i < m; ++i)for (int j = 0; j < n; ++j) {if (grid[i][j] == 1)fresh++;if (grid[i][j] == 2)q.push({i, j});}// 多源 bfswhile (!q.empty() && fresh) {min++; // 当前所有腐烂橘子,同时向 4 个方向扩散for (int size = q.size(); size; --size) {auto node = q.front(); // 队头q.pop();int x = node.first, y = node.second;// 腐烂上下左右(4 个方向)的橘子for (int i = 0; i < 4; ++i) {int xx = x + nex[i][0], yy = y + nex[i][1];// 越界if (xx < 0 || yy < 0 || xx >= m || yy >= n)continue;// 新鲜的才能继续被感染if (grid[xx][yy] == 1) {grid[xx][yy] = 2;fresh--; // 新鲜橘子 -1q.push({xx, yy});}}}}return fresh ? -1 : min;}
};🎂课程表
207. 课程表 - 力扣(LeetCode)
前置知识
1)离散数学:自反,反自反,对称,反对称,出边,入边等概念
2)拓扑排序图解:图-拓扑排序_哔哩哔哩_bilibili
3)图的存储和遍历(DFS,BFS)(👇先看视频,文章看 C++ 代码)
a. 图论基础及遍历算法 | labuladong 的算法笔记
b. 【labuladong】图论基础及遍历算法_哔哩哔哩_bilibili
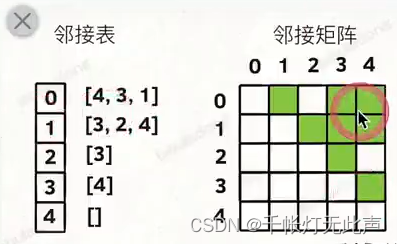
邻接表
vector< vector<int> > graph 或 vector<int> graph[]
表示一个二维动态数组
邻接矩阵
bool matrix[][]
二维静态数组
邻接矩阵:判断 x, y 之间是否有边 O(1),只需 if (matrix[x][y] || martrix[y][x])
邻接表:而邻接表,需要遍历 x 或 y 右边的列表,时间 O(n)
4)拓扑排序:【labuladong】拓扑排序算法及应用_哔哩哔哩_bilibili
5)补充理解:拓扑排序详解(超详细+模板)_拓扑排序模板-CSDN博客
AC BFS
思路
BFS 模拟 拓扑排序:
选择入度 0 的点,加入序列,删除该点和所有出边,更新入度,重复上面两步,直到不存在入度为 0 的点。此时,判断是否所有点都加入序列,如果还有剩余的点,说明有环
(环的存在,导致这部分节点,入度不可能为 0)
要素
1)邻接表:vector< vector<int> > v(动态二维数组)
2)节点的入度:vector<int> in
3)入度为 0 的节点:priority_queue<int, vector<int>, greater<int> > q(最小堆,queue 也可)
坑
第 9,10 行,记得声明 vector 大小为 numCourses
注意,邻接表 x -> y, x -> z, x -> t,所以 x --- y, z, t(以出边为标准)
时间 O(m + n):初始化 = 边数 m(先修课程数) + 拓扑排序 = 节点数 n
空间 O(m + n):队列 n;邻接表 m + n,表头节点 n 个,边数 m
class Solution {
public:// 这里的 prerequisites 先修课程,实际就是 图的点和边bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {int count = numCourses; // 统计入度为 0 课程总数// 初始化:邻接表 和 节点的入度vector<vector<int>> v(numCourses); vector<int> in(numCourses);int n = prerequisites.size();for (int i = 0; i < n; ++i) {// y -> x,y 是 x 的先修课程// 图:节点 y 指向 节点 xint x = prerequisites[i][0], y = prerequisites[i][1];v[y].push_back(x); // 邻接表加边in[x]++; // 节点 x 入度 +1}// 入度为 0 的点加入队列 qpriority_queue<int, vector<int>, greater<int>> q; // 最小堆for (int i = 0; i < numCourses; ++i) if (in[i] == 0) {q.push(i); count--; // 统计是否有环}// 拓扑排序, bfs 逐层扩展while (!q.empty()) {int node = q.top(); // 取入度为 0 的最小节点 nodeq.pop();// 根据邻接表 v[] 在 in[] 删除该点所有出边for (int i = 0; i < v[node].size(); ++i) {int k = v[node][i]; // node -> k,k 的入度 -1in[k]--;if (in[k] == 0) { // 入度为 0q.push(k);count--;}}}return count ? false : true;}
};🌼实现 Trie(前缀树)
208. 实现 Trie (前缀树) - 力扣(LeetCode)
解释
前缀树 == 字典树 == Trie,多叉树的一种(用于高效的前缀匹配)
struct TrieNode {bool isEnd; //该结点是否是一个串的结束TrieNode* next[26]; //字母映射表 };
前缀树,顾名思义,前缀组成的树,上图所示,5 个单词转化为前缀树
l 是根节点,不存放任何数据
坑
第 15,27,39 行,注意移动到下一节点,同时,Trie* node = this,这里的 node 相当于
根节点
代码
m 个字母,插入,查询,前缀匹配,时间复杂度 都是 O(m)
字典树高度 n,最坏情况,不存在前缀相同的单词,空间复杂度 O(m^n)
class Trie {
private:bool isEnd; // 结束标志位vector<Trie*> children; // 下一前缀树节点
public:Trie() : isEnd(false), children(26) {}void insert(string word) {Trie* node = this; // 相当于根节点开始// 遍历单词,类似构造链表,没有该字母,就新建节点for (auto x : word) {int ch = x - 'a'; // 字母偏移量if (node->children[ch] == nullptr)node->children[ch] = new Trie();node = node->children[ch]; // 移动下一节点}node->isEnd = true; }bool search(string word) {Trie* node = this; // 相当于根节点开始// 遍历单词for (auto x : word) {int ch = x - 'a';if (node->children[ch] == nullptr)return false;node = node->children[ch]; // 移动到下一字母}return node->isEnd; // 单词是否结束}bool startsWith(string prefix) {Trie* node = this; // 根节点// 遍历前缀for (auto x : prefix) {int ch = x - 'a';if (node->children[ch] == nullptr)return false;node = node->children[ch]; // 移动到下一字母}return true; // 前缀存在}
};/*** Your Trie object will be instantiated and called as such:* Trie* obj = new Trie();* obj->insert(word);* bool param_2 = obj->search(word);* bool param_3 = obj->startsWith(prefix);*/