提供网站建设收益分录_如何开通公众号_seo外链工具软件_网络营销案例视频

一、SPWM原理

  SPWM其实是相电压的控制方式，定义三相正弦相电压的表达式：
$$\{\begin{array}{cc}{V}_{am}=& V_m\sin \omega t\\ V_{bm}=& V_m\sin (\omega t-\frac{2}{3}\pi )\\ V_{cm}=& V_m\sin (\omega t+\frac{2}{3}\pi )\end{array}$$
  载波比（载波信号频率$f_c$与调制信号频率$f$之比）：
$$m_f=\frac{f_c}{f}$$
  调制深度（调制信号幅值$V_m$与载波信号幅值$V_{sm}$之比）：
$$m_m=\frac{V_m}{V_{sm}}$$
  当载波频率远大于输出电压基波频率 且调制深度 $m_m\le 1$ 时，处于线性调制区域，三相SPWM逆变器相电压的基波幅值满足：
$$V_m=\frac{1}{2}{m}_m{U}_{dc}$$

二、基于零序分量注入的SPWM

• 只介绍均值零序信号

  为了提高直流电压的利用率，在调制波信号中注入零序分量：
$$\{\begin{array}{cc}{V}_{am}=& V_m\sin \omega t+V_0\\ V_{bm}=& V_m\sin (\omega t-\frac{2}{3}\pi )+V_0\\ V_{cm}=& V_m\sin (\omega t+\frac{2}{3}\pi )+V_0\end{array}$$
$V_0$ 的取值范围：$-1-V_{min}\le V_0\le 1-V_{max}$

  均值零序信号：
$$V_0=-\frac{1}{2}(V_{max}+V_{min})$$
注入了一定的高次谐波信号，波顶被削平，因此提高了线性调节范围。

三、MATLAB模型

均值零序信号：

基于零序分量注入的SPWM：

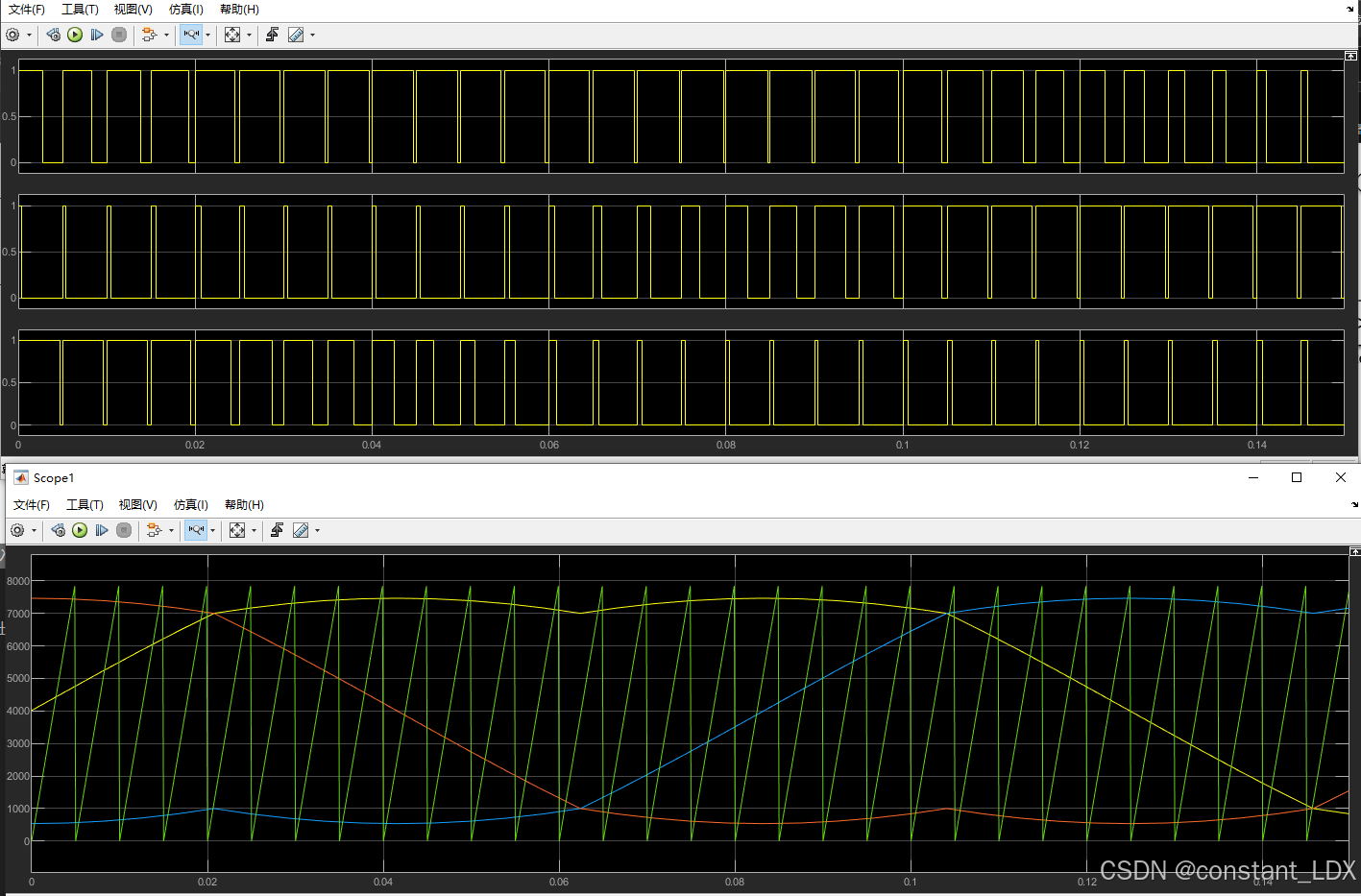
仿真环境模型（模拟MCU的timer输出PWM信号）：

Scope1输出结果与Scope输出结果对应：

主要学习书籍：《现代永磁同步电机控制原理及MATLAB仿真》（部分图片来源）
MATLAB仿真参考资料：《欧拉电子 FOC 用户手册》