手机在线画图工具_seo外包公司接单_广告推广怎么做_seo网站关键字优化

0 专栏介绍

🔥附C++/Python/Matlab全套代码🔥课程设计、毕业设计、创新竞赛必备！详细介绍全局规划(图搜索、采样法、智能算法等)；局部规划(DWA、APF等)；曲线优化(贝塞尔曲线、B样条曲线等)。

🚀详情：图解自动驾驶中的运动规划(Motion Planning)，附几十种规划算法

---

1 有模型PID算法介绍

在

• 轨迹规划 | 图解路径跟踪PID算法(附ROS C++/Python/Matlab仿真)
• 控制原理 | PID控制的三个参数如何影响控制效果？(附参数整定方法)

中我们介绍了无模型PID控制律

$$\Delta u\left(k\right)=K_p\Delta e\left(k\right)+K_{i}e\left(k\right)\Delta t+K_d\left(\Delta e\left(k\right)-\Delta e\left(k-1\right)\right)/\Delta t$$

其优势在于不需要建立复杂的系统模型，便于快速部署；能在不确定性较大的环境中工作，适应系统动态变化；由于不涉及模型计算，控制响应速度快。但缺点也很明显，例如参数调整往往依赖经验，可能需要多次试验；在某些情况下，可能面临系统稳定性问题，特别是在非线性系统中

当我们明确知道系统的动力学模型时，可以考虑采用有模型的PID算法更精确地调整PID参数，优化控制性能

2 基于差速运动学模型的路径跟踪

设系统输出方程

$${\mathbf{x}}_p=\left[\begin{array}{ccc}1& & \\ & 1& \end{array}\right]\mathbf{x}+\mathbf{G}\left(\mathbf{x}\right)$$

其中$\mathbf{x}={\left[\begin{array}{ccc}x& y& \theta \end{array}\right]}^T$，$\mathbf{G}\left(\mathbf{x}\right)={\left[\begin{array}{cc}l\cos \theta & l\sin \theta \end{array}\right]}^T$。${\mathbf{x}}_p$的物理意义是如图所示的前瞻点，$l$是机器人中心距离前瞻点的几何长度。

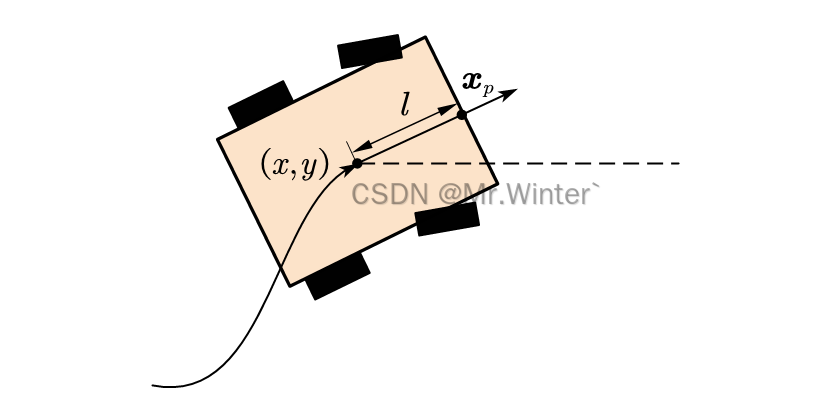
进一步求解输出的一阶微分

$${\dot{\mathbf{x}}}_p=\left[\begin{array}{ccc}1& & \\ & 1& \end{array}\right]\dot{\mathbf{x}}+\mathbf{J}\left(\mathbf{x}\right)$$

其中雅克比矩阵

$$\mathbf{J}\left(\mathbf{x}\right)=\frac{\partial \mathbf{G}\left(\mathbf{x}\right)}{\partial {\mathbf{x}}^T}=\left[\begin{array}{ccc}0& 0& -l\dot{\theta }\sin \theta \\ 0& 0& l\dot{\theta }\cos \theta \end{array}\right]$$

根据建模分析 | 差速轮式移动机器人运动学建模(附Python/Matlab仿真)知道差速移动机器人的运动学方程为

$$\dot{\mathbf{x}}=\left[\begin{array}{c}\dot{x}\\ \dot{y}\\ \dot{\theta }\end{array}\right]=\left[\begin{array}{cc}\cos \theta & 0\\ \sin \theta & 0\\ 0& 1\end{array}\right]\left[\begin{array}{c}v\\ \omega \end{array}\right]=S\left(\mathbf{q}\right)\mathbf{u}$$

整理可得

$${\dot{\mathbf{x}}}_p=\left[\begin{array}{cc}\cos \theta & -l\sin \theta \\ \sin \theta & l\cos \theta \end{array}\right]\mathbf{u}=\mathbf{R}\left(\theta \right)\mathbf{u}$$

进行变量置换$\mathbf{v}=\mathbf{R}\left(\theta \right)\mathbf{u}$，可得线性的输出方程

$${\dot{\mathbf{x}}}_p=\mathbf{v}$$

此时只需设计线性的反馈控制律

$$\mathbf{v}=-\mathbf{K}\left({\mathbf{x}}_p-{\mathbf{x}}_d\right)$$

即可获得线性非齐次微分方程的解

$${\mathbf{x}}_p={\left[\begin{array}{cc}{C}_1{e}^{-k_{1}t}+x_d& C_2{e}^{-k_{2}t}+y_d\end{array}\right]}^T$$

其中$\mathbf{K}=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left(k_1,k_2\right)\left(k_1>0,k_2>0\right)$是反馈矩阵，${\mathbf{x}}_d$是系统期望位置。通过输入输出线性化，${\mathbf{x}}_p$可以收敛到${\mathbf{x}}_d$，控制输入为

$$\mathbf{u}={\mathbf{R}}^{-1}\left(\theta \right)\mathbf{v}$$

其中

$${\mathbf{R}}^{-1}\left(\theta \right)=\left[\begin{array}{cc}\cos \theta & \sin \theta \\ -\sin \theta /l& \cos \theta /l\end{array}\right]$$

这是一个基于差速运动学和误差$\mathbf{e}={\mathbf{x}}_p-{\mathbf{x}}_d$的P控制器

3 微分同胚视角下的有模型PID

流形(manifolds)是可以局部欧几里得空间化的一个拓扑空间，是具有拓扑结构的点集，是欧几里得空间中的曲线、曲面等概念的推广。

欧几里得空间是最简单的流形实例。流形要求拓扑结构的局部为欧式空间或其他相对简单的空间。例如下面的左图所示，在一个半径极大的球面(如地球)上，若以充分大的尺度去度量一个三角形则其只能为曲边三角形，欧式距离不成立，因为位于二维平面上的点不能沿直线穿过球面到达目标点；若以充分小的尺度去度量则可以得到直边三角形——例如在地球上测量跑道长度无需考虑地球的曲率。下面右图中的一维流形同理

一个并非流形的实例是在球面上吊一根线，因为在包含了线和球连接的那一点的附近区域一定不是简单的——既不是线也不是面。

这种将两个流形局部位置的点和几何结构等同起来的方法称为同胚(homeomorphism)，形式化定义为拥有连续逆映射的连续映射；进一步地，定义具有连续可微逆映射的连续可微映射为微分同胚(diffeomorphism)。同胚的概念允许在简单结构上处理复杂问题，利用同胚将非线性问题线性化更精准。本节的输入输出反馈线性化就是微分同胚的例子：当$l>0$时$\mathbf{R}\left(\theta \right)$与${\mathbf{R}}^{-1}\left(\theta \right)$是连续可微的，因此$\mathbf{v}$微分同胚于$\mathbf{u}$

4 算法仿真(ROS C++)

核心代码如下所示：

Eigen::Vector2d PIDController::_pidControl(Eigen::Vector3d s, Eigen::Vector3d s_d, Eigen::Vector2d u_r)
{Eigen::Vector2d u;Eigen::Vector3d e(s_d - s);Eigen::Vector2d sx_dot(k_ * e[0], k_ * e[1]);Eigen::Matrix2d R_inv;R_inv << cos(s[2]), sin(s[2]), -sin(s[2]) / l_, cos(s[2]) / l_;u = R_inv * sx_dot;return u;
}

算法效果如下：

完整工程代码请联系下方博主名片获取

---

🔥 更多精彩专栏：

• 《ROS从入门到精通》
• 《Pytorch深度学习实战》
• 《机器学习强基计划》
• 《运动规划实战精讲》
• …

👇源码获取 · 技术交流 · 抱团学习 · 咨询分享 请联系👇