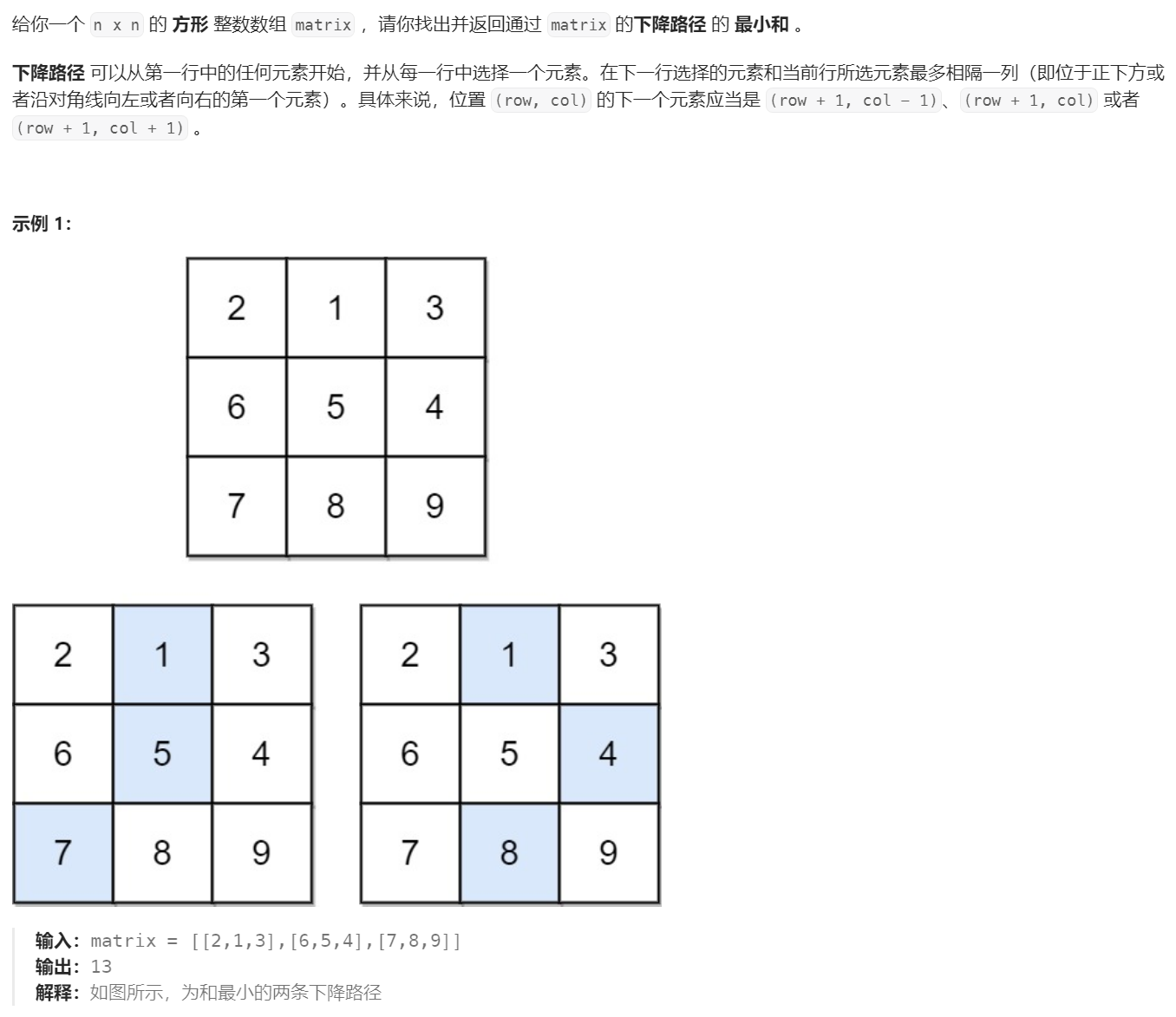
4. 下降路径最小和
931. 下降路径最小和
算法原理
-
确定状态表示
dp[i][j]表示:到达[i, j]位置,最小的下降路径
-
状态转移方程
-
dp[i][j]- 从
[i-1, j-1]到达[i, j]==>dp[i-1][j-1] + m[i][j] - 从
[i-1, j]到达[i, j]==>dp[i-1][j] + m[i][j] - 从
[i-1, i+1]到达[i, j]==>dp[i-1][j+1] + m[i][j]
- 从
-
dp[i][j] = min(上面三个) + m[i][j]
- 初始化
- 目的是为了让我们再填表的过程中不会出现越界的情况
里面的值,要保证后面的填表是正确的
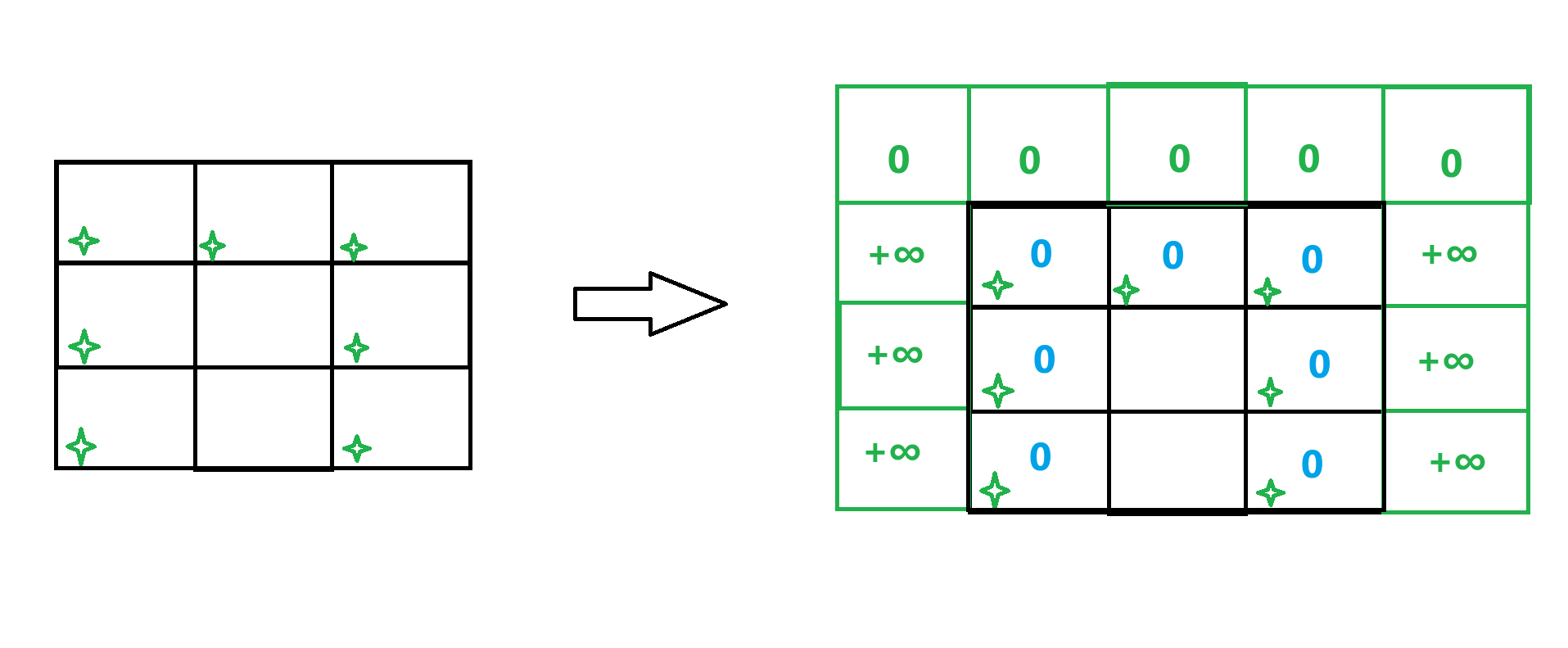
- 绿星的地方都可能会越界
- 进行绿框范围的虚拟节点构造
- 虚拟出的第一行全部填 0,就可以保证原表的第一行都是 0
- 但从原表的第二行开始,每个格子都是取前三者之间的最小值,所以下面虚拟的节点就不能填最小的值 0 了,不然每个格子都是 0。所以都取正无穷大
下标的映射
- 整个表向右下移动了一个单位长度
(0, 0)——>(1, 1)
在初始化的时候,可以把所有虚拟出的节点都设为
+∞,然后将第一行改为0就可以了
-
填表顺序
- 从上往下
-
返回值
- 这里不是返回
dp[m][n]的值 - 返回
dp表中最行一行的最小值
- 这里不是返回
代码编写
public int minFallingPathSum(int[][] matrix) { //1. 创建 dp 表 int n = matrix.length; int[][] dp = new int[n+1][n+2]; //2. 初始化 for (int i = 1; i <= n; i++) { //第一列和最后一列 dp[i][0] = dp[i][n+1] = Integer.MAX_VALUE; } //3. 填表 for (int i = 1; i <= n; i++) { for (int j = 1; j <= n; j++) { dp[i][j] = Math.min(dp[i-1][j], Math.min(dp[i-1][j], dp[i-1][j+1])) + matrix[i-1][j-1]; } } int ret = Integer.MAX_VALUE; for (int i = 1; i <= n; i++) { ret = Math.min(ret, dp[n][i]); } return ret;
}
- 取最值只能两个进行比较
- 注意无穷值的写法
时间复杂度:
n*n(两个for循环)
空间复杂度:n*n(弄了个二维dp表)
5. 最小路径和
64. 最小路径和
算法原理
-
确定状态表示
dp[i][j]表示:到达[i, j]位置时,最小路径和
-
状态转移方程
dp[i][j]- 从
[i-1, j]走过来==>dp[i-1][j] + g[i][j] - 从
[i, j-1]走过来==>dp[i][j-1] + g[i][j] - `dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + g[i][j]
- 从
- 初始化
- 因为是取最小值,所以虚拟的节点要小,以免被误取
- 但起点需要是 0,所以它左边和上面的虚拟节点
dp[0][1]和dp[1][0]需要是 0
-
填表顺序
- 从上往下
- 从左往右
-
返回值
- 返回
dp[m][n]
- 返回
代码编写
public int minPathSum(int[][] grid) { //1. 创建 dp 表 int m = grid.length; int n = grid[0].length; int[][] dp = new int[m+1][n+1]; //2. 初始化 for (int i = 0; i <= n; i++) dp[0][i] = Integer.MAX_VALUE; for (int i = 0; i <= m; i++) dp[i][0] = Integer.MAX_VALUE; dp[0][1] = dp[1][0] = 0; //3. 填表 for (int i = 1; i <= m; i++) { for (int j = 1; j <= n; j++) { dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1]) + grid[i-1][j-1]; } } return dp[m][n];
}
6. 地下城游戏
174. 地下城游戏
算法原理
- 确定状态表示
dp[i][j]表示:从[i, j]位置出发,到达终点,所需的最低初始健康点数
这里不能以
[i, j]为终点构建状态表示,
- 状态转移方程
dp[i][j],此时的点数必须要>=下一个要到的地方 dp 值- 从此处往右走,
x+d[i][j] >= dp[i][j+1],所以x >= dp[i][j+1] - d[i][j]即可 - 从此处往下走,同理
x >= d[i+1][j] - d[i][j]即可
- 从此处往右走,
如果 d[i][j] 太大,就是说在那一格有个很大的血包。减完之后就变成一个负值了(你是一个负血的状态,通过这个格子之后也能顺利通过),这是不符合逻辑的。
- 所以我们要把
dp[i][j]和1放在一起取一下max - 如果算出来是负数,就更新为 1
- 如果是大于等于 1 的数,就保持
- 初始化
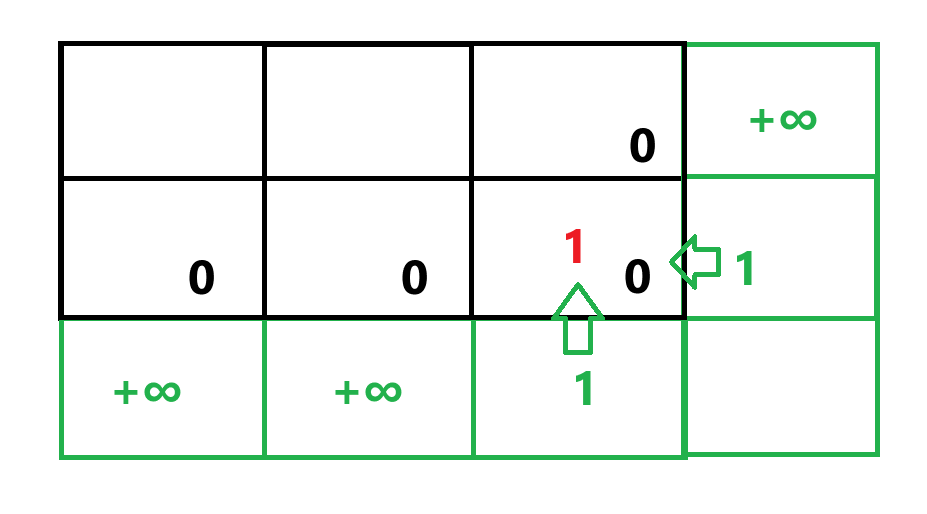
我们关注的是格子的下面和右边的状态,所以可能会越界的是最下面一行和最右边一行
- 我们在最下面和最右边添加辅助节点
- 此时就不用考虑下标映射关系
里面的值,需要保证后续的填表是正确的
- 我们看原表终点格,要走出去,终点最少需要
1点血量 - 所以只需要把终点下面和右边的格子置为
1就可以了 - 其余的位置是两格之间求
min,我们只需要保证辅助的节点不被选上就可以,所以我们将其他的节点设为+∞
-
填表顺序
- 从下往上
- 从右往左
-
返回值
- 返回
dp[0][0]
- 返回
代码编写
public int calculateMinimumHP(int[][] dungeon) { //1. 创建 dp 表 int m = dungeon.length; int n = dungeon[0].length; int[][] dp = new int[m+1][n+1]; //2. 初始化 for (int j = 0; j <= n; j++) dp[m][j] = Integer.MAX_VALUE; for (int i = 0; i <= m; i++) dp[i][n] = Integer.MAX_VALUE; dp[m][n-1] = dp[m-1][n] = 1; //3. 填表 for (int i = m-1; i >= 0; i--) { for (int j = n-1; j >= 0; j--) { dp[i][j] = Math.min(dp[i][j+1], dp[i+1][j]) - dungeon[i][j]; dp[i][j] = Math.max(dp[i][j], 1); } } return dp[0][0];
}